题目内容
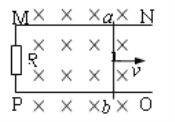
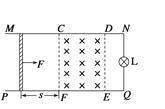
【题目】间距为l的两平行金属导轨由水平部分和倾斜部分平滑连接而成，如图所示，倾角为θ的导轨处于大小为
、方向垂直导轨平面向上的匀强磁场区间Ⅰ中，水平导轨上的无磁场区间静止放置一质量为3m的“联动双杆”（由两根长为l的金属杆cd和ef。用长度为L的刚性绝缘杆连接构成），在“联动双杆”右侧存在大小为
，方向垂直导轨平面向上的匀强磁场区间Ⅱ，其长度大于L，质量为m、长为l的金属杆ab从倾斜导轨上端释放，达到匀速后进入水平导轨（无能量损失），杆ab与“联动双杆”发生碰撞，碰后杆ab和cd粘合在一起形成”联动三杆”，“联动三杆”继续沿水平导轨进入磁场区间Ⅱ并从中滑出，运动过程中，杆ab、cd和ef与导轨始终接触良好，且保持与导轨垂直，已知杆ab、cd和ef电阻均为
，
，
，
，
，
，
，不计摩擦阻力和导轨电阻，忽略磁场边界效应，求：（计算结果均保留两位有效数字）
（1）杆ab在倾斜导轨上匀速运动时的速度大小
；
（2）“联动三杆”进入磁场区间Ⅱ前的速度大小v；
（3）“联动三杆”滑过磁场区间Ⅱ过程中，ef杆产生的焦耳热
。
【答案】（1）
；（2）
；（3）
【解析】
（1）ab杆受到的安培力
感应电流大小
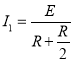
感应电动势
由ab杆匀速运动得
解得
（2）ab杆与联动双杆碰撞过程系统动量守恒，以向右为正方向，由动量守恒定律得
解得
（3）联动三杆进入磁场
过程速度的变化量为
由动量定理得
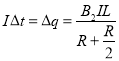
联动三杆离开磁场过程，速度的变化量大小也为
离开磁场时联动三杆的速度
设“联动三杆”滑过磁场区间Ⅱ产生的总焦耳热为Q，由能量守恒定律可知
设ef产生的焦耳热为
，由电路串联关系和焦耳定律可知
解得
练习册系列答案
轻松暑假总复习系列答案
相关题目
