��Ŀ����
����Ŀ����ͼ��ʾ����ֱ������ϵxOyƽ��ĵڢ��������а뾶ΪR��ԲO1�ֱ���x�ᡢy��������P����R��0����Q��0��R�� ���㣬ԲO1�ڴ��ڴ�ֱ��xOyƽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB����y�Ḻ����ƽ�е���ǿ�糡��߽���y���غϣ��ұ߽罻x����M�㣬һ�����������A���������ƣ������Ϊq������Ϊm����ijһ���ʴ�ֱ��x���P������ų������ų�ƫתǡ�ô�Q�����糡������M������x������н�Ϊ45��ķ�������糡����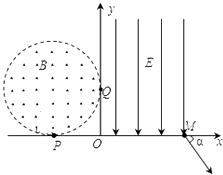
��1��OM֮��ľ��룻
��2������ǿ�糡�ĵ糡ǿ��E��
��3��������һ����A�������͵������ͬ������Ҳ��ͬ������A�䣬��P������x�Ḻ�����30��ǵķ�������ų���������A���ٴλص�x����ij��ʱ���õ������ֵΪ���٣�
���𰸡�
��1���⣺������A����Ϊv0����켣ԲԲ����O�㣬��A�˶���D��ʱ�ٶ���y�ᴹֱ������A��D��G����ƽ���˶���
������ٶ�Ϊa���ڵ糡�����е�ʱ��Ϊt��
���� ![]()
x=OG=v0t ����
�� tan45��= ![]() =
= ![]() ����
����
�����٢ڽ�ã� ![]() =
= ![]() =
= ![]() tan45��=
tan45��= ![]()
����OG=2R����
��OG֮��ľ���2R��
��2���⣺����A�Ĺ켣Բ�뾶ΪR���� ![]()
�� ![]() ����
����
![]() ����
����
�����٢ۢݵ� ![]()
��ã�E= ![]()
�𣺸���ǿ�糡�ĵ糡ǿ�� ![]() ��
��
��3���⣺������A��켣ԲԲ��ΪO�䣬��Ϊ��O��CA��=90�㣬O��C=R���� O��ΪԲ�ģ�RΪ�뾶��A��Ĺ켣Բ��Բ�δų�O1��H�㣬
���ı���CO��H O1Ϊ���Σ���O��H��y�ᣬ����A��Ӵų��г�����y����I�㣬HI��O��H��
��������A��Ҳ�Ǵ�ֱ��y�����糡�ģ�������A���J������糡����x����K�㣬
��������A�ڵ糡�е��˶����ƣ�
��JKG=45�㣬GK=GJ��
OI��JG=R
��OI=R+Rcos30��
��ã�JG=Rcos30��= ![]() R
R
����A���ٴλص�x���ϵ�����Ϊ��2R+ ![]() R��0��
R��0��
��������һ����A�������͵������ͬ������Ҳ��ͬ������A�䣬��C������x�Ḻ�����30��ǵķ�������ų���������A���ٴλص�x����ij��ʱ���õ������ֵΪ��2R+ ![]() R��0����
R��0����
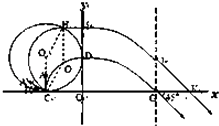
����������1����D��G����ƽ���˶�������ƽ���˶������з������OG֮��ľ��룻��2�������ڴų���������Բ���˶�����Բ���˶��İ뾶��ʾ�����ӵ��ٶȣ����ţ�ٵڶ����ɺ��˶�ѧ��ʽ�����ǿ�糡�ĵ糡ǿ��E����3���������������������A����˶��켣������A��Ҳ�Ǵ�ֱ��y�����糡�ģ���ϼ���֪ʶ�������A���ٴλص�x����ij��ʱ���õ������ֵ��