题目内容
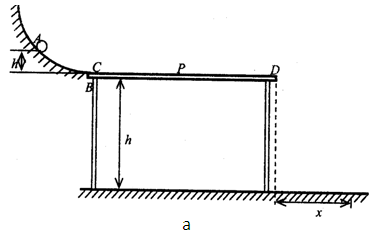
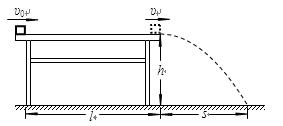
(18分)如图甲所示,粗糙水平面CD与光滑斜面DE平滑连接于D处;可视为质点的物块A、B紧靠一起静置于P点,某时刻A、B在足够大的内力作用下突然分离,此后A向左运动.
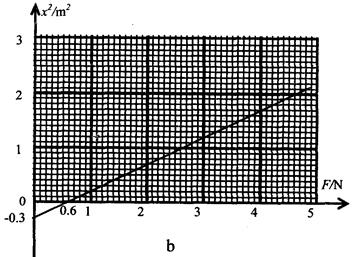
已知:斜面的高度H=1.2m;A、B质量分别为1kg和0.8kg,且它们与CD段的动摩擦因数相同;A向左运动的速度平方与位移大小关系如图乙;重力加速度g取10m/s2.

(1)求A、B与CD段的动摩擦因数 ;
;
(2)求A、B分离时B的速度大小vB;
(3)要使B能追上A,试讨论P、D两点间距x的取值范围.
已知:斜面的高度H=1.2m;A、B质量分别为1kg和0.8kg,且它们与CD段的动摩擦因数相同;A向左运动的速度平方与位移大小关系如图乙;重力加速度g取10m/s2.

(1)求A、B与CD段的动摩擦因数
 ;
;(2)求A、B分离时B的速度大小vB;
(3)要使B能追上A,试讨论P、D两点间距x的取值范围.
见解析
试题分析:解:(1)由图象可知,分离时物块A的初速度vA=4m/s, ①(1分)
A最终位置与P点距离sA=8m, ②(1分)
从A、B分离到A匀减速运动停止,有
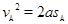 ③(1分)
③(1分)得A的加速度大小 a=1m/s2 ④(1分)
由牛顿第二定律可知
 ⑤(2分)
⑤(2分)解得 μ=0.1 ⑥(2分)
【或:从A、B分离到A匀减速运动停止,由动能定理
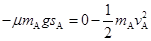 (3分)
(3分)解得 μ=0.1 (1分)】
(2)A、B分离过程,由动量守恒
 ⑦(2分)
⑦(2分)解得 vB="5m/s" ⑧(2分)
(3)(Ⅰ)若B恰好能返回并追上A, B从分离后到追上A过程由动能定理
 ⑨ (2分)
⑨ (2分)解得 x1=2.25m ⑩ (1分)
(Ⅱ)若B恰好不冲出斜面,B从P到E过程由动能定理
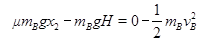 ?(2分)
?(2分)解得 x2=0.50m ? (1分)
综上,要使B能追上A,x应满足:2.25m≥L≥0.50m
(评分说明:①~④各1分,⑤~⑧各2分,⑨?各2分,⑩?各1分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
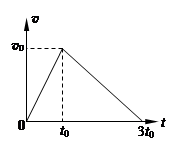
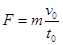
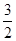 v0t0
v0t0


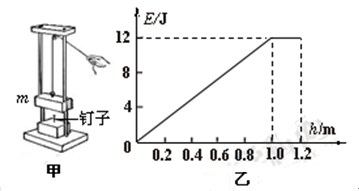
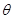 =30o的光滑固定斜面上,放有两个质量分别为1kg和2kg的可视为质点的小球A和B,两球之间用一根长L=0.2m的轻杆相连,小球B距水平面的高度h=0.1m.两球从静止开始下滑到光滑地面上,不计球与地面碰撞时的机械能损失,g取10m/s2.则下列说法中不正确的是( )
=30o的光滑固定斜面上,放有两个质量分别为1kg和2kg的可视为质点的小球A和B,两球之间用一根长L=0.2m的轻杆相连,小球B距水平面的高度h=0.1m.两球从静止开始下滑到光滑地面上,不计球与地面碰撞时的机械能损失,g取10m/s2.则下列说法中不正确的是( ) 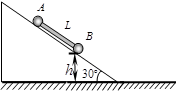
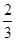 J
J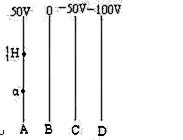
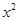 -F的图像,取重力加速度g=10m/s2.
-F的图像,取重力加速度g=10m/s2.