题目内容
17.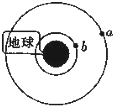 如图,地球赤道正上空有两颗卫星,其中a为地球同步卫星,轨道半径为r,b为另一颗卫星,轨道半径为同步卫星轨道半径的$\frac{1}{\root{3}{16}}$.从图示时刻开始计时,在一昼夜内,两颗卫星共“相遇”的次数为(所谓相遇,是指两颗卫星距离最近)( )
如图,地球赤道正上空有两颗卫星,其中a为地球同步卫星,轨道半径为r,b为另一颗卫星,轨道半径为同步卫星轨道半径的$\frac{1}{\root{3}{16}}$.从图示时刻开始计时,在一昼夜内,两颗卫星共“相遇”的次数为(所谓相遇,是指两颗卫星距离最近)( )| A. | 2次 | B. | 3次 | C. | 4次 | D. | 5次 |
分析 据万有引力提供向心力,结合两卫星的轨道关系,求出b卫星的周期.根据两颗卫星相距最近开始计时到两颗卫星相距最远转过的角度之差等于π求出再次相距最近的时间,即可求解.
解答 解:设地球的质量为M,绕地球运动的卫星的质量为m,轨道半径为R,周期为T,则有
G$\frac{Mm}{{R}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$R
则得 T=2π$\sqrt{\frac{{R}^{3}}{GM}}$
可得b、a两卫星的周期之比为 $\frac{{T}_{b}}{{T}_{a}}$=$\sqrt{\frac{{R}_{b}^{3}}{{R}_{a}^{3}}}$=$\sqrt{\frac{(\frac{1}{\root{3}{16}}r)^{3}}{{r}^{3}}}$=$\frac{1}{4}$
Tb=$\frac{1}{4}{T}_{a}$
a卫星是地球的同步卫星,其周期等于地球自转的周期.
设当两者相距最近开始到再次相距最近时,最少的时间应该满足下式:$\frac{2π}{{T}_{b}}$t-$\frac{2π}{{T}_{a}}$t=2π
则得 t=$\frac{1}{3}{T}_{a}$
所以从图示时刻开始计时,在一昼夜内,两颗卫星相距最近的次数为 n=$\frac{{T}_{a}}{t}$=3(次)
故选:B.
点评 解决本题的关键掌握万有引力提供向心力这一理论,知道周期与轨道半径的关系.以及知道两颗卫星从相距最近到再次相距最近所转过的角度之差等于2π.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 如图所示,边长L=0.2m的正方形线圈abcd,其匝数n=10,总电阻r=2Ω,外电路的电阻R=8Ω,ab边的中点和cd边的中点的连线OO′恰好位于匀强磁场的边界线上,磁场的磁感应强度B=1T,若线圈从图示位置开始计时,以角速度ω=2rad/s 绕OO′轴匀速转动.则以下判断中正确的是( )
如图所示,边长L=0.2m的正方形线圈abcd,其匝数n=10,总电阻r=2Ω,外电路的电阻R=8Ω,ab边的中点和cd边的中点的连线OO′恰好位于匀强磁场的边界线上,磁场的磁感应强度B=1T,若线圈从图示位置开始计时,以角速度ω=2rad/s 绕OO′轴匀速转动.则以下判断中正确的是( )
 如图所示,边长L=0.2m的正方形线圈abcd,其匝数n=10,总电阻r=2Ω,外电路的电阻R=8Ω,ab边的中点和cd边的中点的连线OO′恰好位于匀强磁场的边界线上,磁场的磁感应强度B=1T,若线圈从图示位置开始计时,以角速度ω=2rad/s 绕OO′轴匀速转动.则以下判断中正确的是( )
如图所示,边长L=0.2m的正方形线圈abcd,其匝数n=10,总电阻r=2Ω,外电路的电阻R=8Ω,ab边的中点和cd边的中点的连线OO′恰好位于匀强磁场的边界线上,磁场的磁感应强度B=1T,若线圈从图示位置开始计时,以角速度ω=2rad/s 绕OO′轴匀速转动.则以下判断中正确的是( )| A. | 在t=$\frac{π}{4}$ s时刻,磁场穿过线圈的磁通量最大 | |
| B. | 闭合电路中感应电动势的瞬时值表达式为e=0.8sin 2t V | |
| C. | 从t=0时刻到t=$\frac{π}{4}$ s时刻,通过电阻R的电荷量q=0.02 C | |
| D. | 从t=0时刻到t=$\frac{π}{4}$ s时刻,电阻R上产生的热量为Q=3.2π×10-4 J |
9.在地面上方某一高度有一小球,其重力势能为10J(以地面为参考平面),现让它由静止开始下落,如不计空气阻力,则它在着地前瞬间的机械能为( )
| A. | 30J | B. | 20J | C. | 10J | D. | 0 |
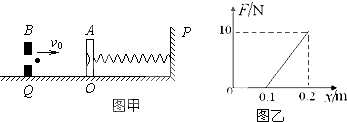
6. 电荷量q=1×10-4C的带正电的小物块静止在绝缘水平面上,所在空间存在沿水平方向的电场,其电场强度E的大小与时间t的关系如图1所示,物块速度v的大小与时间t的关系如图2所示.重力加速度g=10m/s2.则( )
电荷量q=1×10-4C的带正电的小物块静止在绝缘水平面上,所在空间存在沿水平方向的电场,其电场强度E的大小与时间t的关系如图1所示,物块速度v的大小与时间t的关系如图2所示.重力加速度g=10m/s2.则( )
 电荷量q=1×10-4C的带正电的小物块静止在绝缘水平面上,所在空间存在沿水平方向的电场,其电场强度E的大小与时间t的关系如图1所示,物块速度v的大小与时间t的关系如图2所示.重力加速度g=10m/s2.则( )
电荷量q=1×10-4C的带正电的小物块静止在绝缘水平面上,所在空间存在沿水平方向的电场,其电场强度E的大小与时间t的关系如图1所示,物块速度v的大小与时间t的关系如图2所示.重力加速度g=10m/s2.则( )| A. | 物块在4s内位移是8m | B. | 物块的质量是1kg | ||
| C. | 物块与水平面间动摩擦因数是0.4 | D. | 物块在4s内电势能减少了14J |
 要测一个自感系数很大的线圈L的直流电阻RL,实验室提供以下器材:
要测一个自感系数很大的线圈L的直流电阻RL,实验室提供以下器材: 如图示,AOB是$\frac{1}{4}$圆柱玻璃砖的截面,玻璃砖的折射率n=$\sqrt{2}$,一束平行光以45°入射角射入玻璃砖的OA面,这些光线中只有一部分能从圆柱的AB面上射出,假设凡射到OB面的光线全部被吸收,也不考虑OA面的 反射作用,试问圆柱AB面上能射出光线部分占AB表面的几分之几?
如图示,AOB是$\frac{1}{4}$圆柱玻璃砖的截面,玻璃砖的折射率n=$\sqrt{2}$,一束平行光以45°入射角射入玻璃砖的OA面,这些光线中只有一部分能从圆柱的AB面上射出,假设凡射到OB面的光线全部被吸收,也不考虑OA面的 反射作用,试问圆柱AB面上能射出光线部分占AB表面的几分之几?