Question

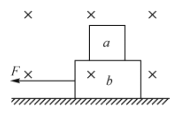
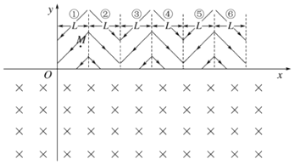
【题目】如图所示，在xOy坐标系中，第三、四象限存在垂直坐标平面向里的匀强磁场，第一象限用虚线分成宽度均为L的①、②、③、④、⑤、⑥……等多个区域，各区域均有平行坐标平面、电场强度大小都为E的匀强电场，区域①、③、⑤……中的电场与x轴负方向成45°角；区域②、④、⑥……中的电场与轴正方向成45°角。一质量为m、带电量为q的带正电的粒子自坐标为（L， L）的M点由静止释放，粒子重力不计，已知第三、四象限匀强磁场的磁感应强度大小为，求：

（1）粒子第一次进人磁场后做圆周运动的半径大小；

（2）写出粒子第二次和第四次与轴交点的坐标，并在答题卡对应的图中画出粒子自开始释放至第四次经过x轴的轨迹；

（3）粒子在运动过程中会经过坐标为（8L，0）的点，自开始释放至到达该点的时间。

Answer 1

【答案】（1）L；（2）（2L，0），（4L，0），轨迹见解析；（3）（7+4π）或（9+4π）。

【解析】

（1）根据勾股定理可知，粒子第一次在电场中的位移大小为L，根据动能定理可得：

qEL=mv2

所以粒子第一次在磁场中的速度大小为：

v=

根据题意可得磁场的磁感应强度大小为

B=

粒子进入磁场后，根据洛伦兹力提供向心力可得：

qvB=m

粒子第一次进入磁场后做圆周运动的半径

；

（2）根据几何关系可知，粒子第二次与x轴交点的坐标为（2L，0），第四次与x轴交点的坐标为（4L，0），自开始释放至第四次与x轴相交的轨迹如图所示；

（3）根据

可得粒子每次在电场中做匀速直线运动的时间为：

根据洛伦兹力提供向心力可得：

qvB=

可得粒子运动周期为：

T=

粒子每次在磁场中转过270°时间为：

t2=

粒子每次在磁场中转过90°时间为：

t3=

自开始释放至到达该点的时间为：

t=7t1+2t2+2t3=

或

=9t1+2t2+2t3=