题目内容
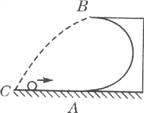
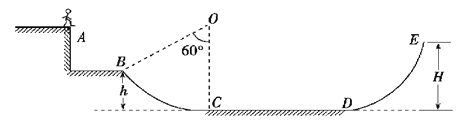
【题目】滑板运动是极限运动的鼻祖,许多极限运动项目均由滑板项目延伸而来.如图所示是滑板运动的轨道,BC和DE是两段光滑圆弧形轨道,BC段的圆心为O点,圆心角为
60°,半径OC与水平轨道CD垂直,水平轨道CD段粗糙且长8 m.一运动员从轨道上的A点以3 m/s的速度水平滑出,在B点刚好沿轨道的切线方向滑入圆弧形轨道BC,经CD轨道后冲上DE轨道,到达E点时速度减为零,然后返回.已知运动员和滑板的总质量为60 kg,B、E两点与水平面CD的竖直高度分别为h和H,且h=2 m,H=2.8 m,g取10 m/s2.求:
(1)运动员从A运动到达B点时的速度大小vB;
(2)轨道CD段的动摩擦因数μ;
(3)通过计算说明,第一次返回时,运动员能否回到B点?如能,请求出回到B点时的速度大小;如不能,则最后停在何处?
【答案】(1)![]() (2)
(2)![]() (3)最后停在D点左侧6.4m处,或C点右侧1.6m处
(3)最后停在D点左侧6.4m处,或C点右侧1.6m处
【解析】试题分析: (1)由题意可知:![]()
解得:![]()
(2)由B点到E点,由动能定理可得:
![]()
由①②带入数据可得:![]()
(3)运动员能到达左侧的最大高度为![]() ,从B到第一次返回左侧最高处,根据动能定理
,从B到第一次返回左侧最高处,根据动能定理![]()
解出![]()
所以:第一次返回时,运动员不能回到B点
设运动员从B点运动到停止,在CD段的总路程为s,由动能定理可得:
![]()
解得:![]()
因为![]() ,所以运动员最后停在D点左侧6.4m处,或C点右侧1.6m处。
,所以运动员最后停在D点左侧6.4m处,或C点右侧1.6m处。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目