题目内容
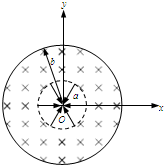 如图所示,半径分别为a、b的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差为U,两圆之间的空间存在垂直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿+x轴方向以很小的初速度逸出,粒子质量为m,电量为q,(不计粒子重力,忽略粒子初速度)求:
如图所示,半径分别为a、b的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差为U,两圆之间的空间存在垂直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿+x轴方向以很小的初速度逸出,粒子质量为m,电量为q,(不计粒子重力,忽略粒子初速度)求:(1)粒子到达小圆周上时的速度为多大?
(2)粒子以(1)中的速度进入两圆间的磁场中,当磁感应强度超过某一临界值时,粒子将不能到达大圆周,求此最小值B.
(3)若磁感应强度取(2)中最小值,且b=(
| 2 |
分析:(1)根据动能定理,通过末动能求出加速电压的大小.
(2)根据洛伦兹力提供向心力,根据牛顿第二定律求出粒子在磁场中运动的轨道半径的表达式,要使粒子不能到达大圆周,其最大的圆半径为轨迹圆与大圆周相切.
(3)根据题目给定的条件,画出带电粒子运动的轨迹,从而确定粒子在磁场中转过φ=270°,然后沿半径进入电场减速到达金属球表面,再经电场加速原路返回磁场,如此重复,恰好经过4个回旋后,沿与原出射方向相反的方向回到原出发点.
(2)根据洛伦兹力提供向心力,根据牛顿第二定律求出粒子在磁场中运动的轨道半径的表达式,要使粒子不能到达大圆周,其最大的圆半径为轨迹圆与大圆周相切.
(3)根据题目给定的条件,画出带电粒子运动的轨迹,从而确定粒子在磁场中转过φ=270°,然后沿半径进入电场减速到达金属球表面,再经电场加速原路返回磁场,如此重复,恰好经过4个回旋后,沿与原出射方向相反的方向回到原出发点.
解答:解:(1)粒子在电场中加速,根据动能定律得:qU=
mv2
所以:v=
(2)粒子进入磁场后,受洛伦兹力做匀速圆周运动,有:
qBv=m
要使粒子不能到达大圆周,其最大的圆半径为轨迹圆与大圆周相切,如图,
则有:
=b-r
所以:r=
联立解得:B =
(3)图中 tanθ=
=
=1即θ=45°
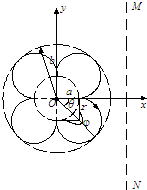
则粒子在磁场中转过φ=270°,然后沿半径进入电场减速到达金属球表面,再经电场加速原路返回磁场,如此重复,恰好经过4个回旋后,沿与原出射方向相反的方向回到原出发点.
因为 T=
将B代入,得粒子在磁场中运动时间为t=4×
T=
答:(1)粒子到达小圆周上时的速度为
;
(2)当磁感应强度超过某一临界值时,粒子将不能到达大圆周,求此最小值B =
;
(3)要粒子恰好第一次沿逸出方向的反方向回到原出发点,粒子需经过4次回旋;粒子在磁场中运动的时间
.
| 1 |
| 2 |
所以:v=
|
(2)粒子进入磁场后,受洛伦兹力做匀速圆周运动,有:
qBv=m
| v2 |
| r |
要使粒子不能到达大圆周,其最大的圆半径为轨迹圆与大圆周相切,如图,
则有:
| a2+r2 |
所以:r=
| b2-a2 |
| 2b |
联立解得:B =
| 2b |
| b2-a2 |
|
(3)图中 tanθ=
| r |
| a |
| b2-a2 |
| 2ab |

则粒子在磁场中转过φ=270°,然后沿半径进入电场减速到达金属球表面,再经电场加速原路返回磁场,如此重复,恰好经过4个回旋后,沿与原出射方向相反的方向回到原出发点.
因为 T=
| 2πm |
| Bq |
将B代入,得粒子在磁场中运动时间为t=4×
| 3 |
| 4 |
| 3π(b2-a2) |
| b |
|
答:(1)粒子到达小圆周上时的速度为
|
(2)当磁感应强度超过某一临界值时,粒子将不能到达大圆周,求此最小值B =
| 2b |
| b2-a2 |
|
(3)要粒子恰好第一次沿逸出方向的反方向回到原出发点,粒子需经过4次回旋;粒子在磁场中运动的时间
| 3π(b2-a2) |
| b |
|
点评:本题粒子在有圆形边界的磁场做匀速圆周运动的问题,画出轨迹,根据几何知识分析临界条件,求半径和圆心角是常用的思路.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一个小球以一定的速度先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开两圆轨道,若小球在两圆轨道的最高点对轨道的压力都恰好为零.
如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一个小球以一定的速度先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开两圆轨道,若小球在两圆轨道的最高点对轨道的压力都恰好为零. 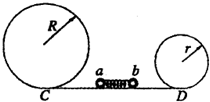 如图所示,半径分别为R和r(R>r)的甲乙两光滑圆轨道安置在同一竖直平面内,两轨道之间由一条光滑水平轨道CD相连,在水平轨道CD上一轻弹簧a、b被两小球夹住,同时释放两小球,a、b球恰好能通过各自的圆轨道的最高点,求:
如图所示,半径分别为R和r(R>r)的甲乙两光滑圆轨道安置在同一竖直平面内,两轨道之间由一条光滑水平轨道CD相连,在水平轨道CD上一轻弹簧a、b被两小球夹住,同时释放两小球,a、b球恰好能通过各自的圆轨道的最高点,求: (2011?信阳二模)如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,又滑上乙轨道,最后离开两圆轨道.通过动摩擦因数为μ的CD段,若小球在两圆轨道的最高点对轨道压力都恰好为零,且CD段的动摩擦因数为μ,试求水平CD段的长度.
(2011?信阳二模)如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,又滑上乙轨道,最后离开两圆轨道.通过动摩擦因数为μ的CD段,若小球在两圆轨道的最高点对轨道压力都恰好为零,且CD段的动摩擦因数为μ,试求水平CD段的长度.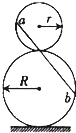 如图所示,半径分别为r和R的圆环竖直叠放(相切)于水平面上,一条公共斜弦过两圆切点且分别与两圆相交于a、b两点.在此弦上铺一条光滑轨道,且令一小球从b点以某一初速度沿轨道向上抛出,设小球穿过切点时不受阻挡.若该小球恰好能上升到a点,则该小球从b点运动到a点所用时间为多少?
如图所示,半径分别为r和R的圆环竖直叠放(相切)于水平面上,一条公共斜弦过两圆切点且分别与两圆相交于a、b两点.在此弦上铺一条光滑轨道,且令一小球从b点以某一初速度沿轨道向上抛出,设小球穿过切点时不受阻挡.若该小球恰好能上升到a点,则该小球从b点运动到a点所用时间为多少?