题目内容
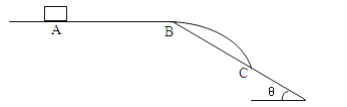
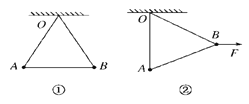
【题目】在某一旅游景区,建有一山坡滑草运动项目。 设山坡AB可看成长度为L=50m、倾角370的斜面,山坡底端与一段水平缓冲段BC圆滑连接。一名游客连同滑草装置总质量m=80kg,滑草装置与AB段及BC段间动摩擦因数均为=0.25。他从A处由静止开始匀加速下滑,通过B点滑入水平缓冲段。 不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8。结果保留2位有效数字。求:

(1)游客在山坡上滑行时的加速度大小;
(2)另一游客站在BC段上离B处60m的P处观看, 通过计算判断该游客是否安全;
(3)AB段游客连同滑草装置所受各个力所做的总功。
【答案】(1) ![]() (2)
(2) ![]() ,不安全 (3)
,不安全 (3) ![]()
【解析】试题根据牛顿第二定律求出游客在山坡上滑行时的加速度大小。对全过程研究,运用动能定理求出游客在BC段上滑行的位移,从而判断游客是否安全;根据功的定义即可求出总功。
(1)设游客在山坡上滑行时加速度大小为a,则有:mgsin370-μmgcos370=ma
解得:a=gsin370-μgcos370=10×0.6-0.25×10×0.8=4m/s2
(2)设PB距离为x,对全过程由动能定理得:mgLsin370-μmgcos370L-μmgx=0
代入数据解得:x=80m,因为x>60m,可知游客不安全。
(3)AB段游客连同滑草装置重力做的功为:![]()
摩擦力做功为:![]()
所以AB段游客连同滑草装置所受各个力所做的总功: ![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目