题目内容
(10分)如图所示,在直角坐标系Oxy平面的第三、四象限内分别存在着垂直于Oxy平面的匀强磁场,第三象限的磁感应强度大小是第四象限的2倍,方向相反。质量、电荷量相同的负粒子a、b,某时刻以大小相同的速度分别从x轴上的P、Q两点沿y轴负方向垂直射入第四、三象限磁场区域。已知a粒子在离开第四象限磁场时,速度方向与y轴的夹角为60o,且在第四象限磁场中运行时间是b粒子在第三象限磁场中运行时间的4倍。不计重力和两粒子之间的相互作用力。
求:a、b两粒子经Y轴时距原点O的距离之比。
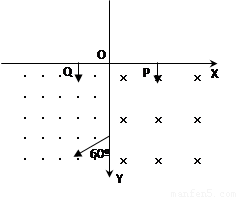
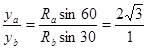
【解析】设第三象限内磁场磁感应强度大小为2B,第四象限内磁场磁感应强度大小为B,粒子a、b质量为m电荷量大小为q进入磁场区域速度为v由洛伦兹力和牛顿第二定律得:
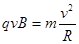 (1分)
(1分)
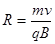 (1分)
(1分)
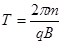 (1分)
(1分)
由题设条件有: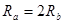
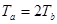 (2分)
(2分)
设b粒子在第三象限中运行时转过的圆心角为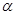 ,由a、b两粒子运行时间关系有:
,由a、b两粒子运行时间关系有:
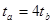 即
即 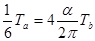 (2分)
(2分)
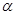 =30º
(1分)
=30º
(1分)
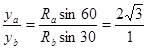 (2分)
(2分)
本题考查带电粒子在磁场中的运动,由洛伦兹力提供向心力可求得半径和周期的表达式,由题干中的已知条件可得半径和周期的关系,结合几何关系可求解

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案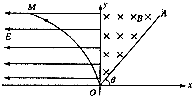 如图所示,在直角坐标平面的第I象限内有一匀强磁场区域,磁感应强度为B,直线OA是磁场右侧的边界.在第Ⅱ象限区域,存在电场强度大小为E的水平向左的匀强电场,y轴是电场、磁场区域的分界线曲线,OM满足方程x=-ky2(k>0).有一带电荷量为q、质量为m的负粒子(重力不计)在曲线OM上某一点由静止释放,穿越y轴进入磁场中.
如图所示,在直角坐标平面的第I象限内有一匀强磁场区域,磁感应强度为B,直线OA是磁场右侧的边界.在第Ⅱ象限区域,存在电场强度大小为E的水平向左的匀强电场,y轴是电场、磁场区域的分界线曲线,OM满足方程x=-ky2(k>0).有一带电荷量为q、质量为m的负粒子(重力不计)在曲线OM上某一点由静止释放,穿越y轴进入磁场中. (2013?怀化二模)如图所示,在直角坐标xOy平面y轴左侧(含y轴)有一沿y轴负向的匀强电场,一质量为m,电量为q的带正电粒子从x轴上P处以速度ν0沿x轴正向进入电场,从y轴上Q点离开电场时速度变为2ν0,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的矩形匀强磁场区域(图中未画出,粒子过Q点继续运动一段距离后才进入磁场区域),磁场磁感应强度大小
(2013?怀化二模)如图所示,在直角坐标xOy平面y轴左侧(含y轴)有一沿y轴负向的匀强电场,一质量为m,电量为q的带正电粒子从x轴上P处以速度ν0沿x轴正向进入电场,从y轴上Q点离开电场时速度变为2ν0,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的矩形匀强磁场区域(图中未画出,粒子过Q点继续运动一段距离后才进入磁场区域),磁场磁感应强度大小 如图所示,在直角坐标xOy平面y轴左侧(含y轴)有一沿y轴负向的匀强电场,一质量为m,电量为q的带正电粒子从x轴上P处以速度v0沿x轴正向进入电场,从y轴上Q点离开电场时速度方向与y轴负向夹角θ=30°,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小B=
如图所示,在直角坐标xOy平面y轴左侧(含y轴)有一沿y轴负向的匀强电场,一质量为m,电量为q的带正电粒子从x轴上P处以速度v0沿x轴正向进入电场,从y轴上Q点离开电场时速度方向与y轴负向夹角θ=30°,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小B= 如图所示,在直角坐标xoy的第一象限中分布着指向-y轴方向的匀强电场,在第四象限中分布着垂直纸面向里方向的匀强磁场,一个质量为m、带电+q的粒子(不计重力)在A点(0,3)以初速V0=120m/s平行x轴射入电场区域,然后从电场区域进入磁场,又从磁场进入电场,并且只通过x轴上的P点(6,0)和Q点(8,0)各一次,已知该粒子的荷质比为q/m=108c/kg.
如图所示,在直角坐标xoy的第一象限中分布着指向-y轴方向的匀强电场,在第四象限中分布着垂直纸面向里方向的匀强磁场,一个质量为m、带电+q的粒子(不计重力)在A点(0,3)以初速V0=120m/s平行x轴射入电场区域,然后从电场区域进入磁场,又从磁场进入电场,并且只通过x轴上的P点(6,0)和Q点(8,0)各一次,已知该粒子的荷质比为q/m=108c/kg. 沿x轴正向进入电场,从y轴上Q点离开电场时速度方向与y轴负向夹角
沿x轴正向进入电场,从y轴上Q点离开电场时速度方向与y轴负向夹角 ,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小
,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小 ,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求:
,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求: