题目内容
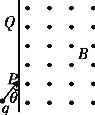
【题目】如图所示,在足够长的竖直线的右侧有方向垂直纸面向外且范围足够大的磁感应强度为B的匀强磁场区域,一带电粒子q从P点沿与竖直线成角θ=45°方向,以大小为v的初速度垂直磁场方向射入磁场中,经时间t从Q点射出磁场。不计粒子重力,下列说法正确的是
A. 粒子射出磁场时与水平线的夹角为θ
B. 带电粒子的比荷q/m=π/Bt
C. 若PQ之间的距离等于L,则带电粒子在匀强磁场中的轨迹半径R=L
D. 带电粒子q可能带正电荷
【答案】A
【解析】
根据粒子在P点的速度方向及P、Q的位置关系得到粒子偏转方向,从而由左手定则得到电性;根据粒子做匀速圆周运动,由几何关系求得离开磁场时的速度方向,轨道半径及中心角,即可根据洛伦兹力做向心力得到周期,从而得到运动时间,进而反解出荷质比。
粒子在磁场中只受洛伦兹力作用,故粒子做匀速圆周运动,则根据几何关系可得粒子射出磁场时与竖直线的夹角θ=45o,所以与水平线的夹角为θ=45o,故A正确;根据粒子做匀速圆周运动,由粒子在P点上方离开磁场可得:粒子做逆时针圆周运动,那么,根据粒子只受洛伦兹力作用,由左手定则可得:粒子带负电,故D错误;粒子做匀速圆周运动,由粒子在P点的速度方向,根据几何关系可得:粒子转过的中心角为90°,若PQ之间的距离等于L,则带电粒子在匀强磁场中的轨迹半径![]() ,根据粒子转过的中心角可得:运动时间
,根据粒子转过的中心角可得:运动时间![]() ,所以,粒子比荷
,所以,粒子比荷![]() ,故BC错误。所以A正确,BCD错误。
,故BC错误。所以A正确,BCD错误。

练习册系列答案
相关题目