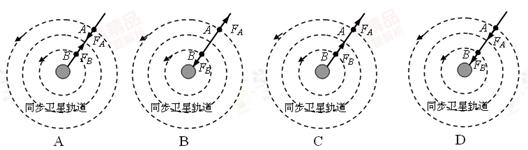
题目内容
如图所示，绝缘轻弹簧的下端固定在斜面底端，弹簧与斜面平行，带电小球Q（可视为质点）固定在光滑绝缘斜面上的M点，且在通过弹簧中心的直线ab上。现把与Q大小相同，电性相同的小球P，从N点由静止释放，在小球P与弹簧接触到压缩到最短的过程中（弹簧始终在弹性限度内），以下说法正确的是
| A．小球P和弹簧组成的系统机械能减小 | B．小球P速度逐渐减小到零 |
| C．小球P的动能与弹簧弹性势能的总和增大 | D．小球P的加速度先减小后增大 |
CD
解析试题分析：小球Q对P做正功，则小球P和弹簧组成的系统机械能增加，A错误，C正确；小球P先沿斜面加速向下运动，当加速度减小到零后，减速向下运动，加速度增大，当弹簧压缩量最大时，小球静止，加速度最大，则小球P的速度先增大后减小．加速度先减小后增大，B错误，D正确。
考点：本题考查系统机械能守恒，牛顿运动定律。
轻松课堂标准练系列答案意大利科学家伽利略在研究物体变速运动规律时，做了著名的“斜面实验”,他测量了铜球在较小倾角斜面上的运动情况，发现铜球做的是匀加速直线运动，且铜球加速度随斜面倾角的增大而增大,在当时的年代由于加速度增大而导致时间无法测定，于是他对大倾角情况进行了合理的外推，由此得出的结论是
| A．自由落体运动是一种匀加速直线运动 |
| B．力是使物体产生加速度的原因 |
| C．力不是维持物体运动的原因 |
| D．物体都具有保持原来运动状态的属性，即惯性 |
如图所示，长为L的细绳一端固定，另一端系一质量为m的小球.给小球一个合适的初速度，小球便可在水平面内做匀速圆周运动，这样就构成了一个圆锥摆，设细绳与竖直方向的夹角为θ．下列说法中正确的是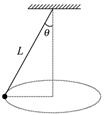 
| A．小球受重力、绳的拉力和向心力作用 |
| B．小球做圆周运动的半径为Lsinθ |
| C．θ 越大，小球运动的速度越大 |
| D．θ 越大，小球所受的合力越小 |
如图甲所示，电阻不计且间距为L=1m的光滑平行金属导轨竖直放置，上端连接阻值为R=1Ω的电阻，虚线OO′下方有垂直于导轨平面向里的匀强磁场．现将质量为m=0.3kg、电阻Rab=1Ω的金属杆ab从OO′上方某处以一定初速释放，下落过程中与导轨保持良好接触且始终水平．在金属杆ab下落0.3m的过程中，其加速度a与下落距离h的关系图象如图乙所示．已知ab进入磁场时的速度v0=3.0m/s，取g=10m/s2．则下列说法正确的是（ ）
| A．进入磁场后，金属杆ab中电流的方向由b到a |
| B．匀强磁场的磁感应强度为2.0T |
| C．金属杆ab下落0.3m的过程中，通过R的电荷量0.24C |
| D．金属杆ab下落0.3m的过程中，R上产生的热量为0.45J |
已知地球的质量约为火星质量的10倍，地球的半径约为火星半径的2倍，则航天器在火星表面附近绕火星做匀速圆周运动的速率约为（ ）
| A．3.5km/s | B．5.0km/s | C．17.7km/s | D．35.2km/s |
如图所示，三个物体质量分别为
=1.0kg、 
=2.0kg、
="3.0kg" ，已知斜面上表面光滑，斜面倾角
，和
之间的动摩擦因数μ=0.8。不计绳和滑轮的质量和摩擦。初始用外力使整个系统静止，当撤掉外力时，
将（g=10m/s2,最大静摩擦力等于滑动摩擦力）( )
| A．和一起沿斜面下滑 |
| B．和一起沿斜面上滑 |
| C．相对于下滑 |
| D．相对于上滑 |
