题目内容
已知地球的质量约为火星质量的10倍,地球的半径约为火星半径的2倍,则航天器在火星表面附近绕火星做匀速圆周运动的速率约为( )
| A.3.5km/s | B.5.0km/s | C.17.7km/s | D.35.2km/s |
A
解析试题分析:设航天器的质量为m,地球的质量为M1,半径为R1,火星的质量为M2,半径为R2,航天器在它们表面附近绕它们运动的速率分别为v1、v′1,其向心力由它们对航天器的万有引力提供,根据牛顿第二定律和万有引力定律有: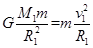 ,
,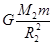 =
=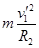 ,解得:
,解得: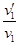 =
=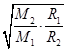 =
=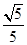 ,在地球表面附近做圆周运动的速度为第一宇宙速度,即:v1=7.9km/s,解得航天器在火星表面附近绕火星做匀速圆周运动的速率约为:v′1=
,在地球表面附近做圆周运动的速度为第一宇宙速度,即:v1=7.9km/s,解得航天器在火星表面附近绕火星做匀速圆周运动的速率约为:v′1=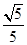 v1=3.5km/s,故选项A正确。
v1=3.5km/s,故选项A正确。
考点:本题主要考查了牛顿第二定律、万有引力定律的应用和第一宇宙速度的识记问题,属于中档题。

如图所示,质量不计的轻质弹性杆P插入桌面上的小孔中,杆的另一端套有一质量为m的小球,今使小球在水平面内做半径为R的匀速圆周运动,角速度为ω.则下列说法正确的是(重力加速度为g) ( )
A.球所受的合外力大小为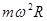 |
B.球所受的合外力大小为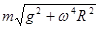 |
C.球对杆作用力的大小为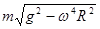 |
D.球对杆作用力的大小为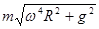 |
如图所示,绝缘轻弹簧的下端固定在斜面底端,弹簧与斜面平行,带电小球Q(可视为质点)固定在光滑绝缘斜面上的M点,且在通过弹簧中心的直线ab上。现把与Q大小相同,电性相同的小球P,从N点由静止释放,在小球P与弹簧接触到压缩到最短的过程中(弹簧始终在弹性限度内),以下说法正确的是
| A.小球P和弹簧组成的系统机械能减小 | B.小球P速度逐渐减小到零 |
| C.小球P的动能与弹簧弹性势能的总和增大 | D.小球P的加速度先减小后增大 |
如图所示,P是位于水平粗糙桌面上的物块,用跨过光滑轻质定滑轮的轻绳将P与钩码Q相连,Q的质量为m,在P向右加速运动的过程中,桌面以上的绳子始终是水平的,关于物体P受到的拉力和摩擦力的以下描述中正确的是 
| A.P受到的拉力的施力物体是钩码Q,大小等于mg |
| B.P受到的拉力的施力物体是绳子,大小等于mg |
| C.P受到的摩擦力方向水平向左,大小一定小于mg |
| D.P受到的摩擦力方向水平向左,大小有可能等于mg |
假想一个登陆舱接近了木星的一个卫星——木卫四的表面。如果发动机提供了一个3260N的向上的推力,登陆舱以恒定速率下降。如果发动机仅提供2200N的推力,登陆舱以0.4m/s2的加速度下降。则登陆舱的质量与靠近木卫四表面的自由下落的加速度分别为
| A.326kg 1.23m/s2 | B. 2650kg 2.46 m/s2 |
| C.2650kg 1.23m/s2 | D. 326kg 2.46.m/s2 |
如图所示,空间存在着与圆台母线垂直向外的磁场,各处的磁感应强度大小均为B,圆台母线与竖直方向的夹角为θ,一个质量为m、半径为r的匀质金属环位于圆台底部。环中维持恒定的电流I不变,圆环由静止向上运动,经过时间t后撤去该恒定电流并保持圆环闭合,圆环全程上升的最大高度为H。已知重力加速度为g,磁场的范围足够大。在圆环向上运动的过程中,下列说法正确的是( )
| A.在时间t内安培力对圆环做功为mgH |
| B.圆环先做匀加速运动后做匀减速运动 |
C.圆环运动的最大速度为 -gt -gt |
| D.圆环先有扩张后有收缩的趋势 |
如图所示,用长为L的轻杆拴着质量为m的小球在竖直平面内做圆周运动,则( )
| A.小球在最高点时所受向心力一定为重力 |
| B.小球在最高点时杆子的拉力不可能为零 |
C.若小球刚好能在竖直面内做圆周运动,则其在最高点速率是 |
| D.小球在圆周最低点时一定对杆子施加向下的拉力,且一定大于重力 |
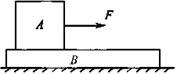
 μmg时,A的加速度为
μmg时,A的加速度为 μg
μg μg
μg ,当升降机突然处于完全失重状态时,则此瞬时AB两物体的瞬时加速度为别为( )
,当升降机突然处于完全失重状态时,则此瞬时AB两物体的瞬时加速度为别为( )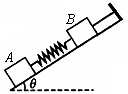
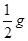 、
、 B.
B. 、
、 D.
D.