题目内容
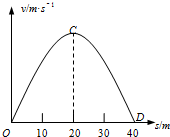 (2007?连云港三模)质量为50kg的小明,在一座高桥上做“蹦极”运动.他所用的轻弹性绳原长为12m,弹性绳中的弹力与弹性绳的伸长量遵循胡克定律,在整个运动中弹性绳不超过弹性限度.小明从桥面下落,能达到距桥面为40m的最低点D处,下落速率v跟下落距离s的关系如图所示,小明在C点时的速度最大.空气阻力不计,重力加速度g取10m/s2.(提示:弹力做功W=
(2007?连云港三模)质量为50kg的小明,在一座高桥上做“蹦极”运动.他所用的轻弹性绳原长为12m,弹性绳中的弹力与弹性绳的伸长量遵循胡克定律,在整个运动中弹性绳不超过弹性限度.小明从桥面下落,能达到距桥面为40m的最低点D处,下落速率v跟下落距离s的关系如图所示,小明在C点时的速度最大.空气阻力不计,重力加速度g取10m/s2.(提示:弹力做功W=. | F |
(1)绳的劲度系数k;
(2)小明到达D点时,绳的弹性势能Ep;
(3)小明到达C点时的速度vC.
分析:(1)在C点速度最大,则C点是平衡位置,则有重力等于弹力,结合胡克定律即可求解;
(2)对由O到D的过程运用机械能守恒定律列式即可求解;
(3)对由O到C的过程,根据动能定理列式即可求解,其中弹簧弹力做功W弹=
x=
△xc
(2)对由O到D的过程运用机械能守恒定律列式即可求解;
(3)对由O到C的过程,根据动能定理列式即可求解,其中弹簧弹力做功W弹=
. |
| F |
| mg |
| 2 |
解答:解:(1)对C点有mg=k△xc
由图可知△xc=sc-s0
带入数据解得:k=62.5N/m
(2)对由O到D的过程运用机械能守恒定律得:
mghD=E弹
代入数据解得:
E弹=2×104J
(3)对由O到C的过程,根据动能定理得:
mghc-W弹=
mvc2
其中W弹=
x=
△xc
解得:vc=8
m/s
答:(1)绳的劲度系数k为62.5N/m;
(2)小明到达D点时,绳的弹性势能为2×104J;
(3)小明到达C点时的速度为8
m/s.
由图可知△xc=sc-s0
带入数据解得:k=62.5N/m
(2)对由O到D的过程运用机械能守恒定律得:
mghD=E弹
代入数据解得:
E弹=2×104J
(3)对由O到C的过程,根据动能定理得:
mghc-W弹=
| 1 |
| 2 |
其中W弹=
. |
| F |
| mg |
| 2 |
解得:vc=8
| 5 |
答:(1)绳的劲度系数k为62.5N/m;
(2)小明到达D点时,绳的弹性势能为2×104J;
(3)小明到达C点时的速度为8
| 5 |
点评:本题主要考查了动能定理、机械能守恒定律、胡克定律的直接应用,要求同学们能清楚物体的运动情况,难度适中.

练习册系列答案
相关题目
 (2007?连云港三模)某兴趣小组对一辆自制遥控小车的性能进行研究,他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段内的图象为曲线外,其余时间段图象均为直线).已知小车运动的过程中,2s~14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行.小车的质量为1kg,可认为在整个过程中小车所受到的阻力大小不变.求:
(2007?连云港三模)某兴趣小组对一辆自制遥控小车的性能进行研究,他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段内的图象为曲线外,其余时间段图象均为直线).已知小车运动的过程中,2s~14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行.小车的质量为1kg,可认为在整个过程中小车所受到的阻力大小不变.求: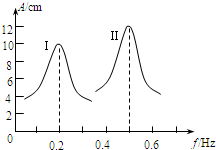 (2007?连云港三模)如图所示为单摆在两次受迫振动中的共振曲线,则下列说法正确的是 ( )
(2007?连云港三模)如图所示为单摆在两次受迫振动中的共振曲线,则下列说法正确的是 ( )