题目内容
12. 如图所示,用一块长L1=1.0m的木板在墙和桌面间架设斜面,桌子高H=0.8m,长L2=1.5m,斜面与水平桌面的倾角θ可在0~60°间调节后固定,将质量m=0.2kg的小物块从斜面顶端静止释放,物块与斜面间的动摩擦因数μ1=0.05,物块与桌面间的动摩擦因数为μ2,忽略物块在斜面与桌面交接处的能量损失(重力加速度取g=10m/s2,最大静止摩擦力等于滑动摩擦力)
如图所示,用一块长L1=1.0m的木板在墙和桌面间架设斜面,桌子高H=0.8m,长L2=1.5m,斜面与水平桌面的倾角θ可在0~60°间调节后固定,将质量m=0.2kg的小物块从斜面顶端静止释放,物块与斜面间的动摩擦因数μ1=0.05,物块与桌面间的动摩擦因数为μ2,忽略物块在斜面与桌面交接处的能量损失(重力加速度取g=10m/s2,最大静止摩擦力等于滑动摩擦力)(1)求θ角增大到多少时,物块能从斜面开始下滑(用正切值表示)
(2)当θ角增大到37°时,物块恰能停在桌面边缘,求物块与桌面间的动摩擦因数μ2(已知sin37°=0.6,cos37°=0.8)
(3)继续增大θ角,发现θ=53°时物块落地点与墙面的距离最大,求此最大距离x.
分析 (1)要使物体下滑重力的分力应大于摩擦力,列出不等式即可求解夹角的正切值;
(2)对下滑过程由动能定理进行分析,则可求得动摩擦因数;
(3)物体离开桌面后做平抛运动,由平抛运动的规律可求得最大距离.
解答 解:(1)为使小物块下滑,则有:
mgsinθ≥μ1mgcosθ;
故θ应满足的条件为:
tanθ≥0.05;
(2)克服摩擦力做功Wf=μ1mgL1cosθ+μ2mg(L2-L1cosθ)
由动能定理得:mgL1sinθ-Wf=0
代入数据解得:
μ2=0.8;
(3)由动能定理得:
mgL1sinθ-Wf=$\frac{1}{2}$mv2
解得:v=1m/s;
对于平抛运动,竖直方向有:
H=$\frac{1}{2}$gt2;
解得:t=0.4s;
水平方向x1=vt
解得:x1=0.4m;
总位移xm=x1+L2=0.4+1.5=1.9m;
答:(1)θ角增大到tanθ≥0.05;,物块能从斜面开始下滑(用正切值表示)
(2)当θ角增大到37°时,物块恰能停在桌面边缘,物块与桌面间的动摩擦因数μ2为0.8;
(3)继续增大θ角,发现θ=53°时物块落地点与墙面的距离最大,此最大距离x为1.9m.
点评 本题考查动能定理及平抛运动的规律,要注意正确分析过程及受力,注意摩擦力的功应分两段进行求解;同时掌握平抛运动的解决方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3. 如图,一充电后的平行板电容器的两极板相距l.在正极板附近有一质量为M、电荷量为q(q>0)的粒子;在负极板附近有另一质量为m、电荷量为-q的粒子.在电场力的作用下,两粒子同时从静止开始运动.已知两粒子同时经过一平行于正极板且与其相距$\frac{2}{5}$l的平面.若两粒子间相互作用力可忽略,不计重力,则M:m为( )
如图,一充电后的平行板电容器的两极板相距l.在正极板附近有一质量为M、电荷量为q(q>0)的粒子;在负极板附近有另一质量为m、电荷量为-q的粒子.在电场力的作用下,两粒子同时从静止开始运动.已知两粒子同时经过一平行于正极板且与其相距$\frac{2}{5}$l的平面.若两粒子间相互作用力可忽略,不计重力,则M:m为( )
 如图,一充电后的平行板电容器的两极板相距l.在正极板附近有一质量为M、电荷量为q(q>0)的粒子;在负极板附近有另一质量为m、电荷量为-q的粒子.在电场力的作用下,两粒子同时从静止开始运动.已知两粒子同时经过一平行于正极板且与其相距$\frac{2}{5}$l的平面.若两粒子间相互作用力可忽略,不计重力,则M:m为( )
如图,一充电后的平行板电容器的两极板相距l.在正极板附近有一质量为M、电荷量为q(q>0)的粒子;在负极板附近有另一质量为m、电荷量为-q的粒子.在电场力的作用下,两粒子同时从静止开始运动.已知两粒子同时经过一平行于正极板且与其相距$\frac{2}{5}$l的平面.若两粒子间相互作用力可忽略,不计重力,则M:m为( )| A. | 3:2 | B. | 2:1 | C. | 5:2 | D. | 3:1 |
7. 如图所示,气垫导轨上滑块经过光电门时,其上的遮光条将光遮住,电子计时器可自动记录遮光时间△t,测得遮光条的宽度为△x,用$\frac{△x}{△t}$近似代表滑块通过光电门时的瞬时速度,为使$\frac{△x}{△t}$更接近瞬时速度,正确的措施是( )
如图所示,气垫导轨上滑块经过光电门时,其上的遮光条将光遮住,电子计时器可自动记录遮光时间△t,测得遮光条的宽度为△x,用$\frac{△x}{△t}$近似代表滑块通过光电门时的瞬时速度,为使$\frac{△x}{△t}$更接近瞬时速度,正确的措施是( )
 如图所示,气垫导轨上滑块经过光电门时,其上的遮光条将光遮住,电子计时器可自动记录遮光时间△t,测得遮光条的宽度为△x,用$\frac{△x}{△t}$近似代表滑块通过光电门时的瞬时速度,为使$\frac{△x}{△t}$更接近瞬时速度,正确的措施是( )
如图所示,气垫导轨上滑块经过光电门时,其上的遮光条将光遮住,电子计时器可自动记录遮光时间△t,测得遮光条的宽度为△x,用$\frac{△x}{△t}$近似代表滑块通过光电门时的瞬时速度,为使$\frac{△x}{△t}$更接近瞬时速度,正确的措施是( )| A. | 换用宽度更窄的遮光条 | B. | 提高测量遮光条宽度的精确度 | ||
| C. | 使滑片的释放点更靠近光电门 | D. | 增大气垫导轨与水平面的夹角 |
1.一渔船向鱼群发出超声波,若鱼群正向渔船靠近,则被鱼群反射回来的超声波与发出的超声波相比( )
| A. | 波速变大 | B. | 波速不变 | C. | 频率变高 | D. | 频率不变 |
11. 一物体原来静止在水平地面上,现有一水平力F拉物体,在F从零开始逐渐增大的过程中,物体先静止,后做变加速运动,其加速度a随外力F变化的图象如图所示,取g=10m/s2,由图可判断该物体( )
一物体原来静止在水平地面上,现有一水平力F拉物体,在F从零开始逐渐增大的过程中,物体先静止,后做变加速运动,其加速度a随外力F变化的图象如图所示,取g=10m/s2,由图可判断该物体( )
 一物体原来静止在水平地面上,现有一水平力F拉物体,在F从零开始逐渐增大的过程中,物体先静止,后做变加速运动,其加速度a随外力F变化的图象如图所示,取g=10m/s2,由图可判断该物体( )
一物体原来静止在水平地面上,现有一水平力F拉物体,在F从零开始逐渐增大的过程中,物体先静止,后做变加速运动,其加速度a随外力F变化的图象如图所示,取g=10m/s2,由图可判断该物体( )| A. | 质量为1kg | B. | 所受的最大静摩擦力为7N | ||
| C. | 所受的滑动摩擦力为7N | D. | 与地面间的动摩擦因数为0.3 |
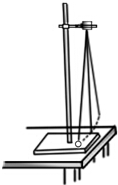 某同学利用单摆测量重力加速度.
某同学利用单摆测量重力加速度. 如图所示,N=50匝的矩形线圈abcd,ab边长l1=20cm,ad边长l2=25cm,放在磁感强度B=0.4T的匀强磁场中,外力使线圈绕垂直于磁感线且通过线圈中线的OO′轴以n=3000r/min的转速匀速转动,线圈电阻r=1Ω,外电路电阻R=9Ω,t=0时,线圈平面与磁感线平行,ab边正转出纸外、cd边转入纸里.
如图所示,N=50匝的矩形线圈abcd,ab边长l1=20cm,ad边长l2=25cm,放在磁感强度B=0.4T的匀强磁场中,外力使线圈绕垂直于磁感线且通过线圈中线的OO′轴以n=3000r/min的转速匀速转动,线圈电阻r=1Ω,外电路电阻R=9Ω,t=0时,线圈平面与磁感线平行,ab边正转出纸外、cd边转入纸里. 如图所示,放在地面上的木块与一劲度系数k=200N/m的轻质弹簧相连,现用手水平拉弹簧,拉力的作用点移动x1=0.2m,木块开始运动,继续拉弹簧,木块缓慢移动了x2=0.4m,求:
如图所示,放在地面上的木块与一劲度系数k=200N/m的轻质弹簧相连,现用手水平拉弹簧,拉力的作用点移动x1=0.2m,木块开始运动,继续拉弹簧,木块缓慢移动了x2=0.4m,求: