题目内容
3. 如图,一充电后的平行板电容器的两极板相距l.在正极板附近有一质量为M、电荷量为q(q>0)的粒子;在负极板附近有另一质量为m、电荷量为-q的粒子.在电场力的作用下,两粒子同时从静止开始运动.已知两粒子同时经过一平行于正极板且与其相距$\frac{2}{5}$l的平面.若两粒子间相互作用力可忽略,不计重力,则M:m为( )
如图,一充电后的平行板电容器的两极板相距l.在正极板附近有一质量为M、电荷量为q(q>0)的粒子;在负极板附近有另一质量为m、电荷量为-q的粒子.在电场力的作用下,两粒子同时从静止开始运动.已知两粒子同时经过一平行于正极板且与其相距$\frac{2}{5}$l的平面.若两粒子间相互作用力可忽略,不计重力,则M:m为( )| A. | 3:2 | B. | 2:1 | C. | 5:2 | D. | 3:1 |
分析 粒子只受到电场力的作用做匀加速直线运动,由牛顿第二定律求出加速度,然后由运动学的公式求出位移,在通过比较位移即可得出它们的质量比.
解答 解:根据题意,两粒子同时经过一平行于正极板且与其相距$\frac{2}{5}$l的平面,所以q的位移为x1=$\frac{2}{5}$l,而-q的位移为:${x}_{2}=l-\frac{2}{5}l=\frac{3}{5}l$
粒子只受到电场力的作用做匀加速直线运动,由牛顿第二定律得:${a}_{1}=\frac{qE}{M}$,
${a}_{2}=\frac{qE}{m}$
又由:$x=\frac{1}{2}a{t}^{2}$
运动的时间是相等的,则:$\frac{{x}_{1}}{{x}_{2}}=\frac{{a}_{1}}{{a}_{2}}=\frac{m}{M}$
所以:$\frac{M}{m}=\frac{{x}_{2}}{{x}_{1}}=\frac{\frac{3}{5}l}{\frac{2}{5}l}=\frac{3}{2}$
故选:A
点评 该题中,粒子都在电场中做匀加速直线运动,运动的时间是相等的,粒子的电荷量又相等,所以并不需要求出具体的数值,写出相应的公式,然后采用比值法即可快速得出结论.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
13.一升降机在箱底装有若干个弹簧,设在一次事故中,升降机的吊索在空中断裂,忽略摩擦力,则升降机从弹簧下端接触地直到最低点的过程中( )
| A. | 升降机加速度不断增大 | |
| B. | 先是弹力做的负功小于重力做的正功,然后是弹力做的负功大于重力做的正功 | |
| C. | 先是弹力做的负功小于重力做的正功,然后是弹力做的负功小于重力做的正功 | |
| D. | 到最低点时,升降机加速度的值大于重力加速度的值 |
14.登上火星是人类的梦想,“嫦娥之父”欧阳自远透露:中国计划于2020年登陆火星.地球和火星公转视为匀速圆周运动,忽略行星自转影响,根据如表,火星和地球相比( )
| 行星 | 半径/m | 质量/kg | 轨道半径/m |
| 地球 | 6.4×106 | 6.0×1024 | 1.5×1011 |
| 火星 | 3.4×106 | 6.4×1023 | 2.3×1011 |
| A. | 火星的公转周期较小 | B. | 火星做圆周运动的加速度较小 | ||
| C. | 火星表面的重力加速度较大 | D. | 火星的第一宇宙速度较大 |
11.我国发射的“嫦娥三号”登月探测器靠近月球后,先在月球表面附近的近似轨道上绕月运行,然后经过一系列过程,在离月面4m高处做一次悬停(可认为是相对于月球静止),最后关闭发动机,探测器自由下落,已知探测器的质量约为1.3×103kg,地球质量约为月球的81倍,地球半径约为月球的3.7倍,地球表面的重力加速度大小约为9.8m/s2,则此探测器( )
| A. | 在着陆前的瞬间,速度大小约为8.9m/s | |
| B. | 悬停时受到的反冲击作用力约为2×103N | |
| C. | 从离开近月圆轨道到着陆这段时间内,机械能守恒 | |
| D. | 在近月圆轨道上运行的线速度小于人造卫星在近地圆轨道上运行的线速度 |
8.下列关于重力势能和弹性势能的相关说法中,正确的是( )
| A. | 重力势能与重力做功密切相关,重力做功与路径有关 | |
| B. | 抬高物体,物体具有重力势能,重力势能是地球上的物体单独具有的 | |
| C. | 弹簧受力发生弹性形变,具有弹性势能,弹性势能是这个力和弹簧共同具有的 | |
| D. | 选择不同的参考平面,重力势能不相同,但是对于同一过程重力势能的变化都是相同的 |
15.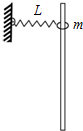 如图所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,且处于原长状态.现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )
如图所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,且处于原长状态.现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )
 如图所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,且处于原长状态.现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )
如图所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,且处于原长状态.现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )| A. | 圆环的机械能守恒 | |
| B. | 弹簧弹性势能变化了$\sqrt{3}$mgL | |
| C. | 圆环下滑到最大距离时,所受合力为零 | |
| D. | 圆环重力势能与弹簧弹性势能之和保持不变 |
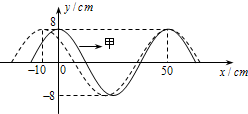 甲、乙两列简谐横波在同一介质中分别沿x轴正向和负向传播,波速均为v=25cm/s,两列波在t=0时的波形曲线如图所示,求:
甲、乙两列简谐横波在同一介质中分别沿x轴正向和负向传播,波速均为v=25cm/s,两列波在t=0时的波形曲线如图所示,求: 如图所示,用一块长L1=1.0m的木板在墙和桌面间架设斜面,桌子高H=0.8m,长L2=1.5m,斜面与水平桌面的倾角θ可在0~60°间调节后固定,将质量m=0.2kg的小物块从斜面顶端静止释放,物块与斜面间的动摩擦因数μ1=0.05,物块与桌面间的动摩擦因数为μ2,忽略物块在斜面与桌面交接处的能量损失(重力加速度取g=10m/s2,最大静止摩擦力等于滑动摩擦力)
如图所示,用一块长L1=1.0m的木板在墙和桌面间架设斜面,桌子高H=0.8m,长L2=1.5m,斜面与水平桌面的倾角θ可在0~60°间调节后固定,将质量m=0.2kg的小物块从斜面顶端静止释放,物块与斜面间的动摩擦因数μ1=0.05,物块与桌面间的动摩擦因数为μ2,忽略物块在斜面与桌面交接处的能量损失(重力加速度取g=10m/s2,最大静止摩擦力等于滑动摩擦力) 如图所示,半径R=0.9m的光滑的半圆轨道固定在竖直平面内,直径AC竖直,下端A与光滑的水平轨道相切.一个质量m=1kg的小球沿水平轨道从A端进入竖直圆轨道,后小球恰好能通过最高点C.不计空气阻力,g取10m/s2.求:
如图所示,半径R=0.9m的光滑的半圆轨道固定在竖直平面内,直径AC竖直,下端A与光滑的水平轨道相切.一个质量m=1kg的小球沿水平轨道从A端进入竖直圆轨道,后小球恰好能通过最高点C.不计空气阻力,g取10m/s2.求: