题目内容
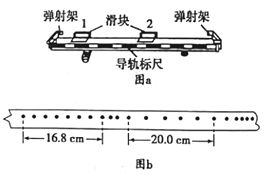
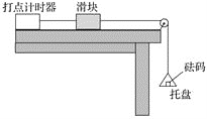
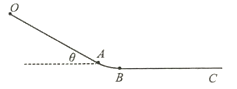
【题目】在丛林探险项目中,缓冲索道简化模型如图所示,现在让质量为m的测试物体(包含挂椅)从O点无初速释放,OA段可看作倾斜直轨道,AB段为第一缓冲区域,在AB段作用下到达B点时速度减小为A点的k倍(k<1),随后进入第二缓冲区水平直索道BC段直至停下,已知OA、BC段与测试物体(包含挂椅)的动摩擦因数都为![]() ,OA段长为l。傾角为
,OA段长为l。傾角为![]() 。求测试物体
。求测试物体
(1)到达A点时的速度大小。
(2)若水平索道足够长,在B点后水平索道上运动的时间。
(3)由于空间限制和追求刺激,在第一缓冲区末端B位置安装撞击减速装置,测试要求在极限情况下撞击过程中的平均加速度大小不能超过重力加速度g的两倍,求极限情况下撞击过程中的减速距离(结果用符号表示)。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)沿OA段下滑的过程由牛顿第二定律得下滑的加速度:
![]()
由速度位移的关系式得:
vA2=2a1l
联立解得:
![]()
(2)由题意知测试物体滑到B点的速度vB=kvA
由牛顿第二定律得测试物体在水平索道上的加速度:
![]()
在水平索道上运动的时间:
![]()
联立解得:
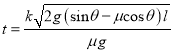
(3)由题意知极限情况下的加速度am=2g
由速度位移的关系式得:
vB2=2amx
联立解得:
![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目