题目内容
1.1mol铜的质量为63.5g,铜的密度是8.9×103kg/m3,试计算(NA=6.02×1023 mol-1)(1)一个铜原子的体积;
(2)假若铜原子为球形,求铜原子的直径;
(3)铜原子的质量.
分析 (1)分子体积=$\frac{摩尔体积}{阿伏加德罗常数}$,摩尔质量=密度×摩尔体积;
(2)根据V=$\frac{1}{6}π{d}^{3}$求解铜原子的直径;
(3)分子质量=$\frac{摩尔质量}{阿伏加德罗常数}$.
解答 解:(1)1 mol铜的体积即摩尔体积
Vm=$\frac{M}{ρ}$=$\frac{6.35×10-2}{8.9×103}$ m3≈7.1×10-6 m3
而1 mol的任何物质中含有NA个粒子,因此每个铜原子的体积为
V0=$\frac{Vm}{NA}$≈1.2×10-29m3.
(2)假设铜原子为球形,其直径为d,根据V=$\frac{1}{6}π{d}^{3}$,铜原子的直径为:
d=$\root{3}{\frac{6V}{π}}=\root{3}{\frac{6×1.89×1{0}^{-29}}{3.14}}$=3.31×10-10m
(3)一个铜原子的质量
m0=$\frac{M}{NA}$=$\frac{6.35×10-2}{6.02×1023}$ kg≈1.05×10-25 kg.
答:(1)一个铜原子的体积是1.2×10-29 m3 (2)假若铜原子为球形,铜原子的直径是2.8×10-10 m;(3)铜原子的重力是1.05×10-25 kg
点评 本题关键要建立物理模型:把固体分子(或原子)当作弹性小球.并假定分子(或原子)是紧密无间隙地堆在一起.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
11.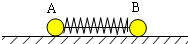 有两个质量不等的物体A、B,静止在光滑的水平面上,它们用细线连着,之间夹着一个被压缩的弹簧.当烧断细线,在弹簧恢复到原长的过程中( )
有两个质量不等的物体A、B,静止在光滑的水平面上,它们用细线连着,之间夹着一个被压缩的弹簧.当烧断细线,在弹簧恢复到原长的过程中( )
 有两个质量不等的物体A、B,静止在光滑的水平面上,它们用细线连着,之间夹着一个被压缩的弹簧.当烧断细线,在弹簧恢复到原长的过程中( )
有两个质量不等的物体A、B,静止在光滑的水平面上,它们用细线连着,之间夹着一个被压缩的弹簧.当烧断细线,在弹簧恢复到原长的过程中( )| A. | 弹簧对两个物体所做的功大小相等 | |
| B. | 弹簧和两个小球组成的系统机械能守恒 | |
| C. | 任何时刻两个物体加速度的大小都相等 | |
| D. | 任何时刻两个物体速度的大小都相等 |
12.力对物体做功的功率,下列说法正确的是( )
| A. | 功率是表示做功快慢的物理量,而不是表示做功大小的物理量 | |
| B. | 力对物体做功的时间越短,这个力的功率就越大 | |
| C. | 力对物体做的功越大,这个力的功率就一定越大 | |
| D. | 力对物体做功少,其功率就小,力对物体做功功多,其功率就大 |
16.在电磁感应现象中,下列说法正确的是( )
| A. | 导体相对磁场运动,导体内一定产生感应电流 | |
| B. | 导体做切割磁感线运动,导体内一定会产生感应电流 | |
| C. | 闭合电路在磁场内做切割磁感线运动,导体内一定会产生感应电流 | |
| D. | 穿过闭合电路的磁通量发生变化,在电路中一定会产生感应电流 |
20.物体做匀加速直线运动,在时间T内通过位移x1到达A点,接着在时间T内又通过位移x2到达B点,则物体( )
| A. | 在A点的速度大小为$\frac{{{x_2}-{x_1}}}{2T}$ | B. | 在B点的速度大小为$\frac{3{x}_{2}-{x}_{1}}{2T}$ | ||
| C. | 运动的加速度为$\frac{2{x}_{1}}{{T}^{2}}$ | D. | 运动的加速度为$\frac{{x}_{1}+{x}_{2}}{{T}^{2}}$ |





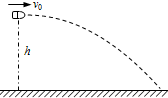 如图所示,质量为3m的炮弹在离地面h=80m高处,以v0=300m/s的水平速度飞行,突然炸裂成质量为2m和m的A、B两个弹片,炸裂后瞬间,弹片A沿着v0原来的方向飞行,速度大小为vA=390m/s.不计空气阻力,取g=10m/s2.求:
如图所示,质量为3m的炮弹在离地面h=80m高处,以v0=300m/s的水平速度飞行,突然炸裂成质量为2m和m的A、B两个弹片,炸裂后瞬间,弹片A沿着v0原来的方向飞行,速度大小为vA=390m/s.不计空气阻力,取g=10m/s2.求: