题目内容
10. 如图所示,质量为3m的炮弹在离地面h=80m高处,以v0=300m/s的水平速度飞行,突然炸裂成质量为2m和m的A、B两个弹片,炸裂后瞬间,弹片A沿着v0原来的方向飞行,速度大小为vA=390m/s.不计空气阻力,取g=10m/s2.求:
如图所示,质量为3m的炮弹在离地面h=80m高处,以v0=300m/s的水平速度飞行,突然炸裂成质量为2m和m的A、B两个弹片,炸裂后瞬间,弹片A沿着v0原来的方向飞行,速度大小为vA=390m/s.不计空气阻力,取g=10m/s2.求:(1)炸裂后瞬间弹片B的速度大小和方向;
(2)两个弹片落地点之间的距离d.
分析 (1)炮弹爆炸过程动量守恒,应用动量守恒定律可以求出另一弹片的速度;
(2)两弹片此后都做平抛运动,根据平抛运动基本公式求解.
解答 解:(1)炮弹爆炸过程动量守恒,以炮弹原飞行方向为正方向,由题意知:v0=300m/s,质量为m的弹片速度为vA=390m/s,质量为2m的单片速度为vB.
由动量守恒定律得:(m+2m)v0=mvA+2mvB,
代入数据解得:vB=120m/s,方向与v0方向相同;
(2)两弹片此后都做平抛运动,则有:
运动时间t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×80}{10}}=4s$,
则两个弹片落地点之间的距离d=(xA-xB)t=1080m
答:(1)炸裂后瞬间弹片B的速度大小为120m/s,方向与v0方向相同;
(2)两个弹片落地点之间的距离d为1080m.
点评 本题考查了平抛运动和动量守恒定律的直接应用,分析清楚题意、应用动量守恒定律与平抛运动基本公式即可正确解题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
20.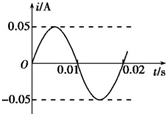 用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )
用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )
 用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )
用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )| A. | 变压器输入功率约为7.9W | |
| B. | 输出电压的最大值是110V | |
| C. | 变压器原、副线圈匝数比是1:2 | |
| D. | 负载电流的函数表达式i=0.05 sin (100πt)A |
1.1mol铜的质量为63.5g,铜的密度是8.9×103kg/m3,试计算(NA=6.02×1023 mol-1)
(1)一个铜原子的体积;
(2)假若铜原子为球形,求铜原子的直径;
(3)铜原子的质量.
(1)一个铜原子的体积;
(2)假若铜原子为球形,求铜原子的直径;
(3)铜原子的质量.
18.质量为m的物体在竖直向上的恒定拉力F作用下,以加速度a=$\frac{g}{3}$匀加速上升h的过程中,下列判断正确的是( )
| A. | 恒定拉力的大小F=$\frac{mg}{3}$ | B. | 物体的机械能增加了$\frac{mgh}{3}$ | ||
| C. | 物体的动能增大了$\frac{mgh}{3}$ | D. | 物体的重力势能增大了$\frac{mgh}{3}$ |
5.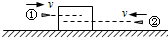 如图所示,光滑水平面上静止有一个木块,一颗子弹以水平速率v向右射向木块,并留在木块中.稍后,另一颗同样的子弹以同样的水平速率v向左射向木块,并留在木块中.下列判断正确的是( )
如图所示,光滑水平面上静止有一个木块,一颗子弹以水平速率v向右射向木块,并留在木块中.稍后,另一颗同样的子弹以同样的水平速率v向左射向木块,并留在木块中.下列判断正确的是( )
 如图所示,光滑水平面上静止有一个木块,一颗子弹以水平速率v向右射向木块,并留在木块中.稍后,另一颗同样的子弹以同样的水平速率v向左射向木块,并留在木块中.下列判断正确的是( )
如图所示,光滑水平面上静止有一个木块,一颗子弹以水平速率v向右射向木块,并留在木块中.稍后,另一颗同样的子弹以同样的水平速率v向左射向木块,并留在木块中.下列判断正确的是( )| A. | 第二颗子弹射入木块并留在木块中后,木块将向左运动 | |
| B. | 第二颗子弹射入木块并留在木块中后,木块将停止运动 | |
| C. | 两次子弹射入过程中的摩擦生热相同 | |
| D. | 第二颗子弹射入木块过程中摩擦生热较多 |
4.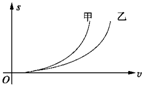 刹车距离是汽车安全性能的重要参数之一.图中所示的图线分别为甲、乙两辆汽车在紧急刹车过程中的刹车距离s与刹车前的车速v的关系曲线,已知紧急刹车过程中车与地面间的摩擦是滑动摩擦.据此可知,下列说法中正确的是( )
刹车距离是汽车安全性能的重要参数之一.图中所示的图线分别为甲、乙两辆汽车在紧急刹车过程中的刹车距离s与刹车前的车速v的关系曲线,已知紧急刹车过程中车与地面间的摩擦是滑动摩擦.据此可知,下列说法中正确的是( )
 刹车距离是汽车安全性能的重要参数之一.图中所示的图线分别为甲、乙两辆汽车在紧急刹车过程中的刹车距离s与刹车前的车速v的关系曲线,已知紧急刹车过程中车与地面间的摩擦是滑动摩擦.据此可知,下列说法中正确的是( )
刹车距离是汽车安全性能的重要参数之一.图中所示的图线分别为甲、乙两辆汽车在紧急刹车过程中的刹车距离s与刹车前的车速v的关系曲线,已知紧急刹车过程中车与地面间的摩擦是滑动摩擦.据此可知,下列说法中正确的是( )| A. | 甲车的刹车距离随刹车前的车速v变化快,甲车的刹车性能好 | |
| B. | 乙车与地面间的动摩擦因数较大,乙车的刹车性能好 | |
| C. | 以相同的车速开始刹车,甲车先停下来,甲车的刹车性能好 | |
| D. | 甲车的刹车距离随刹车前的车速v变化快,甲车与地面间的动摩擦因数较大 |
8.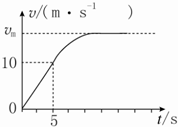 一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.1倍,g取10m/s2,则( )
一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.1倍,g取10m/s2,则( )
 一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.1倍,g取10m/s2,则( )
一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.1倍,g取10m/s2,则( )| A. | 汽车在前5s内的牵引力为6×103N | B. | 汽车在前5s内的牵引力为4×103N | ||
| C. | 汽车的额定功率为50 kW | D. | 汽车的最大速度为20m/s |