题目内容
9.一弹性小球质量为m,自距地面高h处以初速度v0竖直上抛,运动过程中所受空气阻力为f,与地面碰撞时无能量损失,则它最后停在地面上时重力势能的变化为减少了mgh,它在运动停止前通过的总路程为$\frac{{m(2gh+{v^2})}}{2f}$.分析 位移是初位置指向末位置的有向线段,由此确定物体的位移,然后结合重力势能的计算公式W=mgh即可求出物体重力势能的变化;整个的过程中,重力和阻力做功,根据动能定理可算出运动的总路程.
解答 解:从初位置指向末位置的有向线段的长度为h,所以位移为h,物体下降的高度是h,则重力势能减小mgh;
设运动的路程为s,根据动能定理得:
0-$\frac{1}{2}m{v}_{0}^{2}$=mgh-fs
解得:s=$\frac{{m(2gh+{v^2})}}{2f}$
故答案为:减少了mgh,$\frac{{m(2gh+{v^2})}}{2f}$
点评 本题考查重力做功与重力势能改变的关系以及动能定理的应用,解答的关键是区别路程和位移的含义,难度不大,属于基础题.

练习册系列答案
相关题目
20.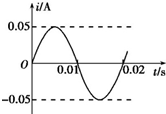 用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )
用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )
 用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )
用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )| A. | 变压器输入功率约为7.9W | |
| B. | 输出电压的最大值是110V | |
| C. | 变压器原、副线圈匝数比是1:2 | |
| D. | 负载电流的函数表达式i=0.05 sin (100πt)A |
4.A、B两小车以细线连在一起放在光滑的水平桌面上,在两车中间有一被压缩的轻弹簧.当细线烧断后,两车被弹开,并在同一时刻撞及桌面边的挡板,此时A车运动了0.6m,B车运动了0.8m,则下列说法中正确的有( )
| A. | 两小车A、B的质量之比为3:4 | |
| B. | 两小车A、B所受冲量大小之比为3:4 | |
| C. | 两小车A、B所受冲力时间之比为3:4 | |
| D. | 细线烧断瞬间,两车的加速度之比为3:4 |
1.1mol铜的质量为63.5g,铜的密度是8.9×103kg/m3,试计算(NA=6.02×1023 mol-1)
(1)一个铜原子的体积;
(2)假若铜原子为球形,求铜原子的直径;
(3)铜原子的质量.
(1)一个铜原子的体积;
(2)假若铜原子为球形,求铜原子的直径;
(3)铜原子的质量.
18.质量为m的物体在竖直向上的恒定拉力F作用下,以加速度a=$\frac{g}{3}$匀加速上升h的过程中,下列判断正确的是( )
| A. | 恒定拉力的大小F=$\frac{mg}{3}$ | B. | 物体的机械能增加了$\frac{mgh}{3}$ | ||
| C. | 物体的动能增大了$\frac{mgh}{3}$ | D. | 物体的重力势能增大了$\frac{mgh}{3}$ |
8.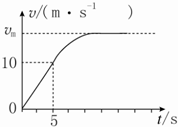 一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.1倍,g取10m/s2,则( )
一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.1倍,g取10m/s2,则( )
 一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.1倍,g取10m/s2,则( )
一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.1倍,g取10m/s2,则( )| A. | 汽车在前5s内的牵引力为6×103N | B. | 汽车在前5s内的牵引力为4×103N | ||
| C. | 汽车的额定功率为50 kW | D. | 汽车的最大速度为20m/s |


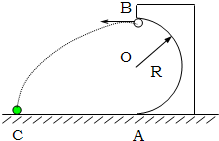 如图所示,半径为R的半圆弧槽固定在水平地面上,质量为m的小球以某速度从A点无摩擦地滚上半圆槽,小球通过最高点B后落到水平地面上的C点,已知AC=AB=2R,求:
如图所示,半径为R的半圆弧槽固定在水平地面上,质量为m的小球以某速度从A点无摩擦地滚上半圆槽,小球通过最高点B后落到水平地面上的C点,已知AC=AB=2R,求: