题目内容
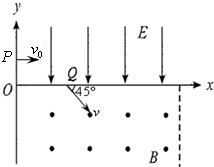 (2013?马鞍山三模)如图,在xoy平面第一象限整个区域分布匀强电场,电场方向平行y轴向下,在第四象限内存在有界匀强磁场,左边界为y轴,右边界为x=
(2013?马鞍山三模)如图,在xoy平面第一象限整个区域分布匀强电场,电场方向平行y轴向下,在第四象限内存在有界匀强磁场,左边界为y轴,右边界为x=| 5 | 2 |
(1)P点坐标;
(2)要使粒子能再进入电场,磁感应强度B的取值范围;
(3)要使粒子能第二次进入磁场,磁感应强度B的取值范围.
分析:(1)粒子在第一象限内做类平抛运动,在x轴方向上做匀速直线运动,在y轴方向做初速度为零的匀加速直线运动,已经知道在Q点时的速度方向为45°,可知此时沿两个坐标轴的速度都是v0,在x轴和y轴分别列式,可求出OP的距离,从而得到P点的坐标
(2)、对粒子在第四象限中的运动轨道进行分析,找到临界状态,即轨道恰好与y轴相切为轨道的最大半径,结合洛伦兹力做向心力的公式可求出此时的磁感应强度,该磁感应强度为最小值,从而可表示出磁感应强度的范围.
(3)、首先要分析粒子恰能第二次进入磁场的轨迹,画出轨迹图,结合轨迹图可求出CQ之间的距离,由几何关系再求出在第四象限内运动轨道的半径,结合洛伦兹力做向心力的公式可求出磁感应强度的最大值,从而可得磁感应强度的范围
(2)、对粒子在第四象限中的运动轨道进行分析,找到临界状态,即轨道恰好与y轴相切为轨道的最大半径,结合洛伦兹力做向心力的公式可求出此时的磁感应强度,该磁感应强度为最小值,从而可表示出磁感应强度的范围.
(3)、首先要分析粒子恰能第二次进入磁场的轨迹,画出轨迹图,结合轨迹图可求出CQ之间的距离,由几何关系再求出在第四象限内运动轨道的半径,结合洛伦兹力做向心力的公式可求出磁感应强度的最大值,从而可得磁感应强度的范围
解答:解:(1)设粒子进入电场时y方向的速度为vy,则vy=v0tan45°
设粒子在电场中运动时间为t,则
OQ=v0t
OP=
t
由以上各式,解得OP=
P点坐标为(0,
)
(2)粒子刚好能再进入电场的轨迹如图所示,设此时的轨迹半径为r1,则
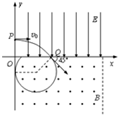
r1+r1sin45°=d 解得:r1=(2-
)d
令粒子在磁场中的速度为v,则v=
根据牛顿第二定律qvB1=
解得:B1=
要使粒子能再进入电场,磁感应强度B的范围 B≥B1
要使粒子刚好从x=2.5d处第二次进入磁场的轨迹如图,
粒子从P到Q的时间为t,则粒子从C到D的时间为2t,所以 CD=2d
CQ=CD-QD=2d-(2.5d-d)=
设此时粒子在磁场中的轨道半径为r2,由几何关系 2r2sin45°=CQ解得 r2=
d
根据牛顿第二定律 qvB2=
解得B2=
要使粒子能第二次进磁场,粒子必须先进入电场,故磁感应强度B要满足B≤B2
综上所述要使粒子能第二次进磁场,磁感应强度B要满足
≤B≤
答:(1)P点的坐标为(0,
)
(2)要使粒子能再进入电场,磁感应强度B的取值范围B≥
(3)磁感应强度B要满足
≤B≤
设粒子在电场中运动时间为t,则
OQ=v0t
OP=
| vy |
| 2 |
由以上各式,解得OP=
| d |
| 2 |
| d |
| 2 |
(2)粒子刚好能再进入电场的轨迹如图所示,设此时的轨迹半径为r1,则

r1+r1sin45°=d 解得:r1=(2-
| 2 |
令粒子在磁场中的速度为v,则v=
| v0 |
| cos45° |
根据牛顿第二定律qvB1=
| mv2 |
| r1 |
(
| ||
| qd |
要使粒子能再进入电场,磁感应强度B的范围 B≥B1
要使粒子刚好从x=2.5d处第二次进入磁场的轨迹如图,
粒子从P到Q的时间为t,则粒子从C到D的时间为2t,所以 CD=2d
CQ=CD-QD=2d-(2.5d-d)=
| d |
| 2 |
设此时粒子在磁场中的轨道半径为r2,由几何关系 2r2sin45°=CQ解得 r2=
| ||
| 4 |
根据牛顿第二定律 qvB2=
| mv2 |
| r2 |
| 4mv0 |
| qd |
要使粒子能第二次进磁场,粒子必须先进入电场,故磁感应强度B要满足B≤B2
综上所述要使粒子能第二次进磁场,磁感应强度B要满足
(
| ||
| qd |
| 4mv0 |
| qd |
答:(1)P点的坐标为(0,
| d |
| 2 |
(2)要使粒子能再进入电场,磁感应强度B的取值范围B≥
(
| ||
| qd |
(3)磁感应强度B要满足
(
| ||
| qd |
| 4mv0 |
| qd |
点评:带电粒子在电场中的运动,综合了静电场和力学的知识,分析方法和力学的分析方法基本相同.先分析受力情况再分析运动状态和运动过程,然后选用恰当的规律解题.解决这类问题的基本方法有两种,第一种利用力和运动的观点,选用牛顿第二定律和运动学公式求解;第二种利用能量转化的观点,选用动能定理和功能关系求解.经对本题的分析可知,粒子在第一象限内做类平抛运动,第一问还可以用能量进行求解.
本题第四象限内存在着有界磁场,带电粒子在第四象限内运动时,受到洛伦兹力的作用,将做有临界状态的圆周运动,对临界状态的寻找与分析成为了解决此类为题的重点和难点.此种类型的题能充分考查考生的综合分析能力和应用数学处理物理问题的能力.解此类问题的关键是做出带电粒子运动的轨迹图,抓住物理过程变化的转折点(列出对应的状态方程),找出粒子运动的半径与磁场边界的约束关系.
本题第四象限内存在着有界磁场,带电粒子在第四象限内运动时,受到洛伦兹力的作用,将做有临界状态的圆周运动,对临界状态的寻找与分析成为了解决此类为题的重点和难点.此种类型的题能充分考查考生的综合分析能力和应用数学处理物理问题的能力.解此类问题的关键是做出带电粒子运动的轨迹图,抓住物理过程变化的转折点(列出对应的状态方程),找出粒子运动的半径与磁场边界的约束关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 (2013?马鞍山三模)如图所示,A、B为均匀带电细圆环中轴线上的两点,O为圆环圆心,B点与O的距离小于A点与O的距离,若圆环所带电荷为正电荷,无穷远处电势为零,下列说法正确的是( )
(2013?马鞍山三模)如图所示,A、B为均匀带电细圆环中轴线上的两点,O为圆环圆心,B点与O的距离小于A点与O的距离,若圆环所带电荷为正电荷,无穷远处电势为零,下列说法正确的是( ) (2013?马鞍山三模)如图所示一列简谐横波在t=0时的波形图,若波的传播速度为2m/s,此时质点P向y轴正方向振动,P、Q两个质点的平衡位置相距一个波长.下列说法正确的是( )
(2013?马鞍山三模)如图所示一列简谐横波在t=0时的波形图,若波的传播速度为2m/s,此时质点P向y轴正方向振动,P、Q两个质点的平衡位置相距一个波长.下列说法正确的是( ) (2013?马鞍山三模)如图所示,A是一质量为m的盒子,B的质量为
(2013?马鞍山三模)如图所示,A是一质量为m的盒子,B的质量为 (2013?马鞍山三模)如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1,金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件不可能求得( )
(2013?马鞍山三模)如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1,金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件不可能求得( )