题目内容
【题目】如图所示的坐标系xOy中，x＜0，y＞0的区域内有沿x轴正方向的匀强电场，x≥0的区域内有垂直于xOy坐标平面向外的匀强磁场，X轴上A点坐标为（﹣L，0），Y轴上B点的坐标为（0， 
L）．有一个带正电的粒子从A点以初速度vA沿y轴正方向射入匀强电 场区域，经过B点进入匀强磁场区域，然后经x轴上的C点 （图中未画出）运动到坐标原点O．不计重力．求：
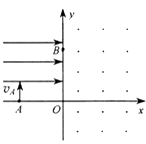
（1）粒子在B点的速度vB是多大？
（2）C点与O点的距离xc是多大？
（3）匀强电场的电场强度与匀强磁场的磁感应强度的比值是多大？
【答案】
（1）解：设粒子在A到B的过程中运动时间为t，在B点时速度沿x轴正方向的速度大小为vx，则
．
．
．
解得vB=2vA
答：粒子在B点的速度vB是2vA
（2）解：设粒子在B点的速度vB与y轴正方向的夹角为θ，则
解得θ=60°
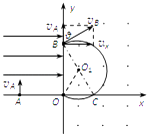
粒子在x≥0的区域内做匀速圆周运动，运动轨迹如图所示，设轨道半径为R，由几何关系有
xc=2Rcosθ
xc= 
（或者通过判断BC 是直径，△OO1C是等边三角形，由xc=R得到xc= ）
答：C点与O点的距离xc是
（3）解：设匀强电场强度为E，匀强磁场的磁感应强度为B，粒子质量为m，带电荷量为q，则
解得 
答：匀强电场的电场强度与匀强磁场的磁感应强度的比值是 
【解析】（1）粒子垂直电场射入，做类平抛运动，在y轴方向上做匀速直线运动，在x轴方向上做匀速直线运动，根据运动学公式求出粒子在B点沿x轴方向上的速度，根据勾股定理求出B点的速度．（2）将B点的速度进行分解，求出B点速度与y轴方向上的夹角，作出带电粒子在磁场中的运动轨迹，根据几何关系求出轨道半径的大小，再根据几何关系确定C点到O点的距离．（3）根据动能定理求出电场强度与B点速度的关系，根据洛伦兹力提供向心力，结合轨道半径的大小，求出磁感应强度与B点速度的关系，从而求出电场强度与磁感应强度的比值．
