题目内容
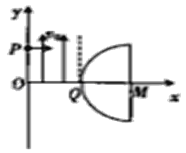
【题目】如图所示，在直角坐标系的第一象限0≤x≤R区域内有沿
轴正方向的匀强电场，右侧有个以坐标为（2R,0）的M点为圆心、半径为R的半圆形区域内有垂直纸面向里的匀强磁场（图中未面出）。现有一质量为m，带电荷量为e的电子，从y轴上的P点以速度v沿x轴正方向射入电场，飞出电场后恰能从坐标为（R,0）的Q点进入半圆形区域，且此时电子的速度方向与x轴正方向的夹角为30°，电子穿出半国形区域时的速度方向垂直于x轴，不考虑电子所受的重力，下列说法正确的是
A.电子进人半圆形区域时的速度大小为
B.匀强电场的电场强度大小
C.半圆形区域内匀强磁场的磁感应强度
的大小为
D.电子刚穿出半圆形区域时的位置坐标为
【答案】C
【解析】
A．电子在匀强电场中做类平抛运动，电子进入圆形区域时的速度大小为
故A错误；
B．电子沿y轴方向的速度分量
＝
①
又
＝
②
根据牛顿第二定律，有
＝
③
＝
④
联立①②③④，得
故B错误；
C．轨迹如图，
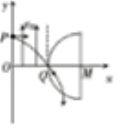
根据图中几何关系可得电子在匀强磁场中做匀速圆周运动的半径为，由
＝
故
故C正确；
D．根据几何关系可得电子穿出半圆形匀强磁场区域时的位置坐标为
＝
故D错误；
练习册系列答案
阳光课堂课时作业系列答案
相关题目
