题目内容
【题目】如图所示,质量分别为mA=0.2kg、mB=0.1kg的A、B两物块叠放在竖直轻弹簧上静止(B与弹簧连接,A、B间不粘连),弹簧的劲度k=20N/m。若给A一个竖直向上的拉力F,使A由静止开始以加速度a=2m/s2向上做匀加速运动。已知弹簧弹性势能的表达式为Ep=![]() kx2(k为弹簧的劲度系数,x为弹簧的形变量)。重力加速度g取10m/s2。求:
kx2(k为弹簧的劲度系数,x为弹簧的形变量)。重力加速度g取10m/s2。求:
(1)B上升高度h为多大时A、B恰好分离;
(2)从开始运动到A、B分离,拉力做的功WF;
(3)定性画出B运动到最高点的过程中其加速度a与位移l的关系图像。(以B初态静止的位置为位移零点)

【答案】(1)0.09m;(2)0.135J;(3)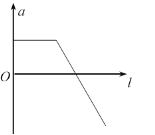
【解析】
(1)初态时,AB整体受力平衡,由平衡条件得
![]()
对B利用牛顿第二定律有
![]()
B上升的高度
![]()
解得
![]()
(2)设A、B分离的速度为v,由运动学公式得
![]()
初态时,弹簧的弹性势能
![]()
分离时,弹簧的弹性势能
![]()
对A、B和弹簧组成的系统,由能量守恒定律得
![]()
解得
![]()
(3)以B初态静止的位置为位移零点,B运动到最高点的过程中其加速度a与位移l的关系图像如图:

练习册系列答案
相关题目