题目内容
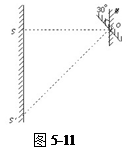
如图5-11所示，S 为一点光源，M为一平面镜，光屏与平面镜平行放置.SO是垂直照射在M上的光线，已知SO=L，若M以角速度ω绕O点逆时针匀速转动，则转过30°角时，光点 S′在屏上移动的瞬时速度v为多大？
解析:
由几何光学知识可知：当平面镜绕O逆时针转过30°时，则：∠SOS′=60°，
OS′=L/cos60°.
选取光点S′为连结点，因为光点 S′在屏上，该点运动方向不变，故该点实际速度（合速度）就是在光屏上移动速度v；光点S′又在反射光线OS′上，它参与沿光线OS′的运动.速度v1和绕O点转动，线速度v2；因此将这个合速度沿光线OS′及垂直于光线 OS′的两个方向分解，由速度矢量分解图5′—1可得：
v1=vsin60°,v2=vcos60°
又由圆周运动知识可得：当线OS′绕O转动角速度为2ω.
则：v2=2ωL/cos60°
vcos60°=2ωL/cos60°,v=8ωL.
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
为多少时,C与B点的水平距离s最大,最大值是多少.
R处，重力加速度取g=10 m/s2.求：
