题目内容
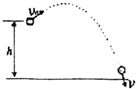 如图所示,人在高度h的地方,斜向上抛出一质量为m的物体,物体到最高点时的速度为v0,落地速度为v,空气阻力不能忽略.则整个过程中重力做的功
如图所示,人在高度h的地方,斜向上抛出一质量为m的物体,物体到最高点时的速度为v0,落地速度为v,空气阻力不能忽略.则整个过程中重力做的功mgh
mgh
,物体克服空气阻力做的功| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:根据W=mg△h求解重力所做的功,根据动能定理求解阻力做的功,进而求出克服阻力做的功.
解答:解:根据W=mg△h得:
重力做的功W=mgh
整个过程中运用动能定理得:
mv2-
mv02=mgh+Wf
解得:Wf=
mv2-
mv02-mgh
所以物体克服空气阻力做的功W克=-Wf=
mv02+mgh-
mv2
故答案为:mgh、
mv02+mgh-
mv2
重力做的功W=mgh
整个过程中运用动能定理得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:Wf=
| 1 |
| 2 |
| 1 |
| 2 |
所以物体克服空气阻力做的功W克=-Wf=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:mgh、
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了重力做功公式及动能定理的直接应用,难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
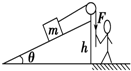 人通过滑轮将质量为m的物体,沿粗糙的斜面由静止开始匀加速地由底端拉上斜面,物体上升的高度为h,到达斜面顶端的速度为v,如图所示.则在此过程中( )
人通过滑轮将质量为m的物体,沿粗糙的斜面由静止开始匀加速地由底端拉上斜面,物体上升的高度为h,到达斜面顶端的速度为v,如图所示.则在此过程中( )A、物体所受的合外力做功为mgh+
| ||
B、物体所受的合外力做功小于
| ||
| C、人对物体做的功为mgh | ||
| D、人对物体做的功大于mgh |
 在海滨游乐场有一种滑沙的娱乐活动.如图所示,人坐在滑板上从斜坡的高处A点由静止开始下滑,滑到斜坡底部B点后沿水平滑道再滑行一段距离到C点停下来,斜坡滑道与水平滑道间是平滑连接的,滑板与两滑道间的动摩擦因数均为μ=0.5,不计空气阻力,重力加速度g=10m/s2,斜坡倾角θ=37°.
在海滨游乐场有一种滑沙的娱乐活动.如图所示,人坐在滑板上从斜坡的高处A点由静止开始下滑,滑到斜坡底部B点后沿水平滑道再滑行一段距离到C点停下来,斜坡滑道与水平滑道间是平滑连接的,滑板与两滑道间的动摩擦因数均为μ=0.5,不计空气阻力,重力加速度g=10m/s2,斜坡倾角θ=37°.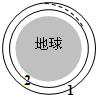 2005年,我国自行研制的“神州六号”载人飞船顺利升空,飞行总时间115小时32分,共绕地球73圈.飞船升空后,首先沿椭圆轨道运行,其近地点离开地面约200公里,远地点离开地面约347公里.在绕地球飞行四圈后,地面发出指令,使飞船上的发动机在飞船到达远地点时自动点火,提高了飞船的速度,实施变轨,使得飞船在距地面h=340公里的圆轨道上飞行.已知地球半径R、地球表面重力加速度g.
2005年,我国自行研制的“神州六号”载人飞船顺利升空,飞行总时间115小时32分,共绕地球73圈.飞船升空后,首先沿椭圆轨道运行,其近地点离开地面约200公里,远地点离开地面约347公里.在绕地球飞行四圈后,地面发出指令,使飞船上的发动机在飞船到达远地点时自动点火,提高了飞船的速度,实施变轨,使得飞船在距地面h=340公里的圆轨道上飞行.已知地球半径R、地球表面重力加速度g.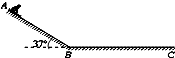 在海滨游乐场里有一种滑沙的游乐活动.如图所示,人坐在滑板上从斜坡的A处由静止开始滑下,滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来.若某人和滑板的总质量m=60.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数相同,大小为μ=0.50,斜坡的倾角θ=37°.斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2.试求:
在海滨游乐场里有一种滑沙的游乐活动.如图所示,人坐在滑板上从斜坡的A处由静止开始滑下,滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来.若某人和滑板的总质量m=60.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数相同,大小为μ=0.50,斜坡的倾角θ=37°.斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2.试求: