题目内容
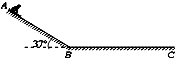 在海滨游乐场里有一种滑沙的游乐活动.如图所示,人坐在滑板上从斜坡的A处由静止开始滑下,滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来.若某人和滑板的总质量m=60.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数相同,大小为μ=0.50,斜坡的倾角θ=37°.斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2.试求:
在海滨游乐场里有一种滑沙的游乐活动.如图所示,人坐在滑板上从斜坡的A处由静止开始滑下,滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来.若某人和滑板的总质量m=60.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数相同,大小为μ=0.50,斜坡的倾角θ=37°.斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2.试求:(1)人从斜坡滑下的加速度为多大?
(2)若出于场地的限制,水平滑道的最大距离为 L=20.0m,则人在斜坡上滑下的距离AB应不超过多少?
(3)若AB间距离为40m,设水平地面为零重力势能面,当人通过斜坡滑道上P点时,其动能恰与重力势能相等,求P点相对水平地面的高度h.(sin37°=0.6,cos37°=0.8)
分析:(1)根据牛顿第二定律求出人从斜坡滑下的加速度大小.
(2)对全程运用动能定理,抓住初末速度为零,求出人在斜坡上滑下的距离AB最小距离.
(3)根据动能定理,结合动能和 重力势能相等求出P点相对水平地面的高度.
(2)对全程运用动能定理,抓住初末速度为零,求出人在斜坡上滑下的距离AB最小距离.
(3)根据动能定理,结合动能和 重力势能相等求出P点相对水平地面的高度.
解答:解:(1)根据牛顿第二定律得,a=
=gsin37°-μgcos37°=10×0.6-0.50×10×0.8m/s2=2m/s2.
(2)根据动能定理得,mgLABsin37°-μmgLABcos37°-μmgL=0-0.
代入数据解得,LAB=6m.
(3)设P点离地面的高度为h.
根据动能定理得,mg(LABsin37°-h)-μmgcos37°(LAB-
)=
mv2-0
又
mv2=mgh
联立两式解得h=6m.
答:(1)人从斜坡滑下的加速度为a1=2m/s2
(2)人在斜坡上滑下的距离AB应不超过50m
(3)P点相对水平地面的高度h=6m.
| mgsin37°-μmgcos37° |
| m |
(2)根据动能定理得,mgLABsin37°-μmgLABcos37°-μmgL=0-0.
代入数据解得,LAB=6m.
(3)设P点离地面的高度为h.
根据动能定理得,mg(LABsin37°-h)-μmgcos37°(LAB-
| h |
| sin37° |
| 1 |
| 2 |
又
| 1 |
| 2 |
联立两式解得h=6m.
答:(1)人从斜坡滑下的加速度为a1=2m/s2
(2)人在斜坡上滑下的距离AB应不超过50m
(3)P点相对水平地面的高度h=6m.
点评:运用动能定理解题首先要确定研究对象和研究过程,分析过程中有哪些力做功,根据动能定理列式求解.

练习册系列答案
相关题目
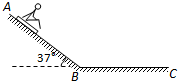 如图所示,在海滨游乐场里有一种滑沙运动.某人坐在滑板上从斜坡的高处A点由静止开始滑下,滑到斜坡底端B点后,沿水平的滑道再滑行一段距离到C点停下来.若人和滑板的总质量m=70.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.50,斜坡的倾角θ=37°(sin37°=0.6,cos37°=0.8),斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2.求:
如图所示,在海滨游乐场里有一种滑沙运动.某人坐在滑板上从斜坡的高处A点由静止开始滑下,滑到斜坡底端B点后,沿水平的滑道再滑行一段距离到C点停下来.若人和滑板的总质量m=70.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.50,斜坡的倾角θ=37°(sin37°=0.6,cos37°=0.8),斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2.求: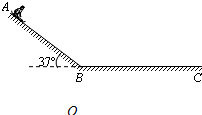 (2009?广州三模)(1)在海滨游乐场里有一种滑沙的游乐活动.如图所示,人坐在滑板上从斜坡的高处由静止开始滑下,滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来.若某人和滑板的总质量m=60.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数相同,大小为μ=0.50,斜坡的倾角θ=37°.斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计.试求:人从斜坡滑下的加速度为多大?若出于场地的限制,水平滑道的最大距离为L=20.0m,则人在斜坡上滑下的距离AB应不超过多少?(sin37°=0.6,cos37°=0.8)
(2009?广州三模)(1)在海滨游乐场里有一种滑沙的游乐活动.如图所示,人坐在滑板上从斜坡的高处由静止开始滑下,滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来.若某人和滑板的总质量m=60.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数相同,大小为μ=0.50,斜坡的倾角θ=37°.斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计.试求:人从斜坡滑下的加速度为多大?若出于场地的限制,水平滑道的最大距离为L=20.0m,则人在斜坡上滑下的距离AB应不超过多少?(sin37°=0.6,cos37°=0.8)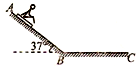 在海滨游乐场里有一种滑沙运动.如图所示,人坐在滑板上从斜坡的某一高处A点由静止开始滑下,滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来.若某人和滑板的总质量m=60.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.50,斜坡的倾角θ=370(sin37°=0.6,cos37°=0.8 ),斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s.求:
在海滨游乐场里有一种滑沙运动.如图所示,人坐在滑板上从斜坡的某一高处A点由静止开始滑下,滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来.若某人和滑板的总质量m=60.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.50,斜坡的倾角θ=370(sin37°=0.6,cos37°=0.8 ),斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s.求: 如图所示,在海滨游乐场里有一种滑沙运动.某人坐在滑板上从斜坡的高处A点由静止开始滑下,滑到斜坡底端B点后,沿水平的滑道再滑行一段距离到C点停下来.若人和滑板的总质量m=60kg,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.50,斜坡的倾角θ=37°(sin37°=0.6,cos37°=0.8),斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2.求:
如图所示,在海滨游乐场里有一种滑沙运动.某人坐在滑板上从斜坡的高处A点由静止开始滑下,滑到斜坡底端B点后,沿水平的滑道再滑行一段距离到C点停下来.若人和滑板的总质量m=60kg,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.50,斜坡的倾角θ=37°(sin37°=0.6,cos37°=0.8),斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2.求: