题目内容
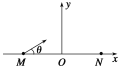
【题目】如图所示,在匀强电场中建立直角坐标系xOy,y轴竖直向上,一质量为m、电荷量为+q的微粒从x轴上的M点射出,方向与x轴夹角为θ,微粒恰能以速度v做匀速直线运动,重力加速度为g.
(1)求匀强电场场强E;
(2)若再叠加一圆形边界的匀强磁场,使微粒能到达x轴上的N点,M、N两点关于原点O对称,距离为L,微粒运动轨迹也关于y轴对称.已知磁场的磁感应强度大小为B,方向垂直xOy平面向外,求磁场区域的最小面积S及微粒从M运动到N的时间t.
【答案】(1)![]() ,方向竖直向上 (2)
,方向竖直向上 (2)![]()
![]() +
+![]()
【解析】
试题分析: (1)对微粒有qE-mg=0,得E=![]()
方向竖直向上.
(2)微粒在磁场中有qvB=m![]() ,解得R=
,解得R=![]() .
.
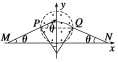
如图所示,当PQ为圆形磁场的直径时,圆形磁场面积最小.有r=Rsin θ
其面积S=πr2=![]()
又T=![]() (或T=
(或T=![]() )
)
根据几何关系可知偏转角为2θ
则在磁场中运动的时间t2=![]() T=
T=![]()
又MP=QN=![]() ,且有t1=t3=
,且有t1=t3=![]()
故运动的时间t=t1+t2+t3=![]() +
+![]() =
=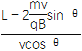 +
+![]() =
=![]() +
+![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目