题目内容
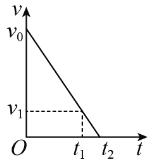
【题目】长为l的轻绳上端固定,下端系着质量为![]() 的小球A,处于静止状态。A受到一个水平瞬时冲量后在竖直平面内做圆周运动,恰好能通过圆周轨迹的最高点。当A回到最低点时,质量为
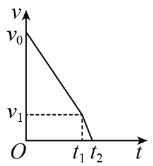
的小球A,处于静止状态。A受到一个水平瞬时冲量后在竖直平面内做圆周运动,恰好能通过圆周轨迹的最高点。当A回到最低点时,质量为![]() 的小球B与之迎面正碰,碰后A、B粘在一起,仍做圆周运动,并能通过圆周轨迹的最高点。不计空气阻力,重力加速度为g,求
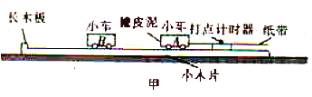
的小球B与之迎面正碰,碰后A、B粘在一起,仍做圆周运动,并能通过圆周轨迹的最高点。不计空气阻力,重力加速度为g,求
(1)A受到的水平瞬时冲量I的大小;
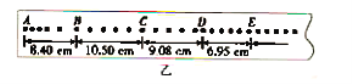
(2)碰撞前瞬间B的动能![]() 至少多大?
至少多大?
【答案】(1)![]() ;(2)
;(2)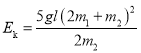
【解析】
(1)A恰好能通过圆周轨迹的最高点,此时轻绳的拉力刚好为零,设A在最高点时的速度大小为v,由牛顿第二定律,有
![]() ①
①
A从最低点到最高点的过程中机械能守恒,取轨迹最低点处重力势能为零,设A在最低点的速度大小为![]() ,有
,有
![]() ②
②
由动量定理,有
![]() ③
③
联立①②③式,得
![]() ④
④
(2)设两球粘在一起时速度大小为![]() ,A、B粘在一起后恰能通过圆周轨迹的最高点,需满足
,A、B粘在一起后恰能通过圆周轨迹的最高点,需满足
![]() ⑤
⑤
要达到上述条件,碰后两球速度方向必须与碰前B的速度方向相同,以此方向为正方向,设B碰前瞬间的速度大小为![]() ,由动量守恒定律,有
,由动量守恒定律,有
![]() ⑥
⑥
又
![]() ⑦
⑦
联立①②⑤⑥⑦式,得碰撞前瞬间B的动能![]() 至少为
至少为
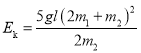 ⑧
⑧

练习册系列答案
相关题目