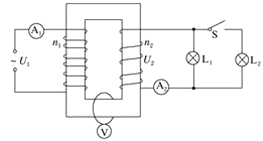
题目内容
【题目】如图所示,ABDO是处于竖直平面内的光滑轨道,AB是半径为R=15 m的 ![]() 圆周轨道,半径OA处于水平位置,BDO是直径为15 m的半圆轨道,D为BDO轨道的中央。一个小球P从A点的正上方距水平半径OA高H处自由落下,沿竖直平面内的轨道运动,离开AB轨道时对轨道末端B点的压力大小等于其重力的
圆周轨道,半径OA处于水平位置,BDO是直径为15 m的半圆轨道,D为BDO轨道的中央。一个小球P从A点的正上方距水平半径OA高H处自由落下,沿竖直平面内的轨道运动,离开AB轨道时对轨道末端B点的压力大小等于其重力的![]() 倍,取g=10 m/s2,求:
倍,取g=10 m/s2,求:
(1)H的大小;
(2)试讨论此球能否到达BDO轨道的O点,并说明理由;
(3)小球从H高处自由落下沿轨道运动后再次落到轨道上的速度大小是多少?

【答案】(1)10m;(2)可以通过;(3)17.3m/s
【解析】
(1)设小球通过D点的速度为v,则有:
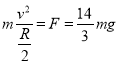 ,
,
小球从P点落下直到沿光滑轨道运动的过程中,机械能守恒,有:
![]() ,
,
可得高度:
![]() ;
;
(2)设小球能够沿竖直半圆轨道运动到O点的最小速度为![]() ,有:
,有:
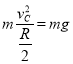 ,
,
小球至少应从![]() 高处落下,
高处落下,
![]() ,
,
解得:
![]() ,
,
由![]() ,小球可以通过O点;
,小球可以通过O点;
(3)小球由H落下通过O点的速度为:
![]() ,
,
小球通过O点后作平抛运动,设小球经时间t落到AB圆弧轨道上,有:
![]() ,
,![]() ,
,
且:
![]() ,
,
可解得时间t=1s(另解舍弃),落到轨道上速度的大小:
![]() 。
。

练习册系列答案
相关题目