题目内容
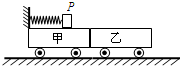 如图所示,光滑水平面上放置质量均为M=2kg的甲、乙两辆小车,两车之间通过一感应开关相连(当滑块滑过两车连接处时,感应开关使两车自动分离,分离时对两车及滑块的瞬时速度没有影响),甲车上表面光滑,乙车上表面与滑块P之问的动摩擦因数μ=0.5,一根轻质弹簧固定在甲车的左端,质量为m=1kg的滑块P(可视为质点)与弹簧的右端接触但不相连,用一根细线拴在甲车左端和滑块P之间使弹簧处于压缩状态,此时弹簧的弹性势能E0=10J,弹簧原长小于甲车长度,整个系统处于静止状态.现剪断细线,滑块P滑上乙车后最终未滑离乙车,g取10m/s2.求:
如图所示,光滑水平面上放置质量均为M=2kg的甲、乙两辆小车,两车之间通过一感应开关相连(当滑块滑过两车连接处时,感应开关使两车自动分离,分离时对两车及滑块的瞬时速度没有影响),甲车上表面光滑,乙车上表面与滑块P之问的动摩擦因数μ=0.5,一根轻质弹簧固定在甲车的左端,质量为m=1kg的滑块P(可视为质点)与弹簧的右端接触但不相连,用一根细线拴在甲车左端和滑块P之间使弹簧处于压缩状态,此时弹簧的弹性势能E0=10J,弹簧原长小于甲车长度,整个系统处于静止状态.现剪断细线,滑块P滑上乙车后最终未滑离乙车,g取10m/s2.求:(1)滑块P滑上乙车前的瞬时速度的大小;
(2)滑块P滑上乙车后相对乙车滑行的距离.
分析:(1)、因地面光滑,所以滑块P在甲车上滑动的过程中,符合动量守恒的条件,同时除了弹簧的弹力做功之外,没有其他的力做功,所以机械能也是守恒的,分别应用动量守恒和机械能守恒列式求解,可得出滑块P滑上乙时的瞬时速度.
(2)、滑块P滑上乙车时,甲乙两车脱离,滑块和乙车做成了系统,经对其受力分析,合外力为零,动量守恒,可求出滑块和乙车的最终共同速度,由能量的转化和守恒可知,系统减少的机械能转化为了内能,即为摩擦力与相对位移的乘积.从而可求出相对位移,即滑块P在乙车上滑行的距离.
(2)、滑块P滑上乙车时,甲乙两车脱离,滑块和乙车做成了系统,经对其受力分析,合外力为零,动量守恒,可求出滑块和乙车的最终共同速度,由能量的转化和守恒可知,系统减少的机械能转化为了内能,即为摩擦力与相对位移的乘积.从而可求出相对位移,即滑块P在乙车上滑行的距离.
解答:解:(1)设滑块P滑上乙车前的速度为v,以整体为研究对象,作用的过程中动量和机械能都守恒,选向右的方向为正,应用动量守恒和能量关系有:
mv1-2Mv2=0…①
E0=
m
-
(2M
…②
①②两式联立解得:v1=4m/s v2=1m/s
(2)以滑块和乙车为研究对象,选向右的方向为正,在此动过程中,由动量守恒定律得:
mv1-Mv2=(m+M)v共…③
由能量守恒定律得:μmgL=
+
-
(M+m)
…④
③④联立并代入得:L=
m
答:①滑块P滑上乙时的瞬时速度的大小为4m/s.
②滑块P滑上乙车后最终未滑离乙车,滑块P在乙车上滑行的距离为
m.
mv1-2Mv2=0…①
E0=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| )v | 2 2 |
①②两式联立解得:v1=4m/s v2=1m/s
(2)以滑块和乙车为研究对象,选向右的方向为正,在此动过程中,由动量守恒定律得:
mv1-Mv2=(m+M)v共…③
由能量守恒定律得:μmgL=
| 1 |
| 2 |
| mv | 2 1 |
| 1 |
| 2 |
| Mv | 2 2 |
| 1 |
| 2 |
| v | 2 共 |
③④联立并代入得:L=
| 5 |
| 3 |
答:①滑块P滑上乙时的瞬时速度的大小为4m/s.
②滑块P滑上乙车后最终未滑离乙车,滑块P在乙车上滑行的距离为
| 5 |
| 3 |
点评:本题考察了动量守恒.机械能守恒和能量的转化与守恒.
应用动量守恒定律解题要注意“四性”,①、系统性.②、矢量性.③、同时性.
机械能守恒的条件是只有重力(或弹簧的弹力)做功,并只发生动能和势能的转化.
应用动量守恒定律解题要注意“四性”,①、系统性.②、矢量性.③、同时性.
机械能守恒的条件是只有重力(或弹簧的弹力)做功,并只发生动能和势能的转化.

练习册系列答案
相关题目
 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求: 如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
 (2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求:
(2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求: 如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )
如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )