题目内容
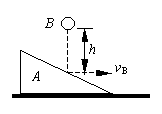
如图所示,一个带斜面的物体A静止在光滑的水平面上,它的质量为M=0.5kg。另一个质量为m =0.2kg的小物体B从高处自由下落,落到B的斜面上,下落高度为h="1.75" m。与斜面碰撞后B的速度变为水平向右,大小为5m/s。(计算时取g="10" m/s2)
①碰后A的速度是多大?
②碰撞过程中A.B的动量变化量各多大?
①- 2 m/s ②-1kg·m/s,其中负号代表方向向左; 1.5 kg·m/s,
方向斜向右上,与水平方向夹角为θ=arctan(v0/vB)=55.3°
①我们规定向右为正方向,设碰后A的速度大小是vA,列水平方向动量守恒的关系式 MvA + mvB = 0,
解出 vA= -mvB/M= - 2 m/s。(负号表示方向向左)
②碰撞过程中A的动量变化量是
ΔpA=MVA= -1kg·m/s,其中负号代表方向向左。
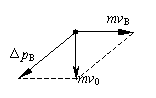
由于B的初、末动量不在同一直线上,不能简单地用正负号表示方向,求动量变化需利用平行四边形定则,如图所示,初动量大小为mv0=
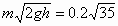 kg·m/s="1.2" kg·m/s,方向竖直向下,末动量大小为mvB=1kg·m/s,方向水平向右,动量变化量的大小为
kg·m/s="1.2" kg·m/s,方向竖直向下,末动量大小为mvB=1kg·m/s,方向水平向右,动量变化量的大小为ΔpB=
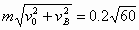 kg·m/s="1.5" kg·m/s,
kg·m/s="1.5" kg·m/s,方向斜向右上,与水平方向夹角为θ=arctan(v0/vB)=55.3°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
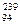 Pu经过 次α衰变和 次β衰变,最后变成铅的同位素 。(填入铅的三种同位素
Pu经过 次α衰变和 次β衰变,最后变成铅的同位素 。(填入铅的三种同位素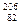 Pb、
Pb、 Pb、
Pb、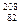 Pb中的一种)
Pb中的一种)
 的质量为
的质量为 ,底部长度为
,底部长度为 ,放在水平面上,盒内有一质量为
,放在水平面上,盒内有一质量为 可视为质点的物体
可视为质点的物体 ,
, ,开始时二者均静止,
,开始时二者均静止, ,以后物体
,以后物体 (
( )后也停止运动。
)后也停止运动。 ,求此时矩形盒
,求此时矩形盒
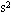 ,求R=?
,求R=?