题目内容
如图所示,竖直平面(纸面)内有直角坐标系xOy,x轴沿水平方向.在x≤O的区域内存在方向垂直于纸面向里,磁感应强度大小为B1的匀强磁场.在第二象限紧贴y轴固定放置长为l、表面粗糙的不带电绝缘平板,平板平行于x轴且与x轴相距h.在第一象限内的某区域存在方向相互垂直的匀强磁场(磁感应强度大小为B2、方向垂直于纸面向外)和匀强电场(图中未画出).一质量为m、不带电的小球Q从平板下侧A点沿x轴正向抛出;另一质量也为m、带电量为q的小球P从A点紧贴平板沿x轴正向运动,变为匀速运动后从y轴上的D点进入电磁场区域做匀速圆周运动,经
圆周离开电磁场区域,沿y轴负方向运动,然后从x轴上的K点进入第四象限.小球P、Q相遇在第四象限的某一点,且竖直方向速度相同.设运动过程中小球P电量不变,小球P和Q始终在纸面内运动且均看作质点,重力加速度为g.求:
(1)匀强电场的场强大小,并判断P球所带电荷的正负;
(2)小球Q的抛出速度vo的取值范围;
(3)B1是B2的多少倍?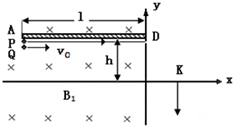
| 1 |
| 4 |
(1)匀强电场的场强大小,并判断P球所带电荷的正负;
(2)小球Q的抛出速度vo的取值范围;
(3)B1是B2的多少倍?

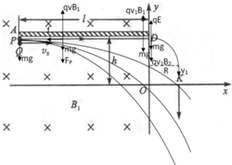
据题意 受力分析 如图所示
(1)带电小球P在电磁复合场中做匀速圆周运动
有 mg=qE ①
即E=
| mg |
| q |
由于小球P变为匀速的从第二象限进入第一象限
由 平衡条件
有 qv1B1=mg ③
由 左手定则 可知 P球带正电.
(2)据题意 Q球与P球恰好在K点相遇 v0有最大值v0mQ球做平抛运动 有
L+R=v0mt ④h=
| 1 |
| 2 |
P球在电磁复合场中做匀速圆周运动
有 qv1B2=m
| ||
| R |
解得 v0m=(L+
| m2g |
| q2B1B2 |
|
即v0的取值范围为 v0<(L+
| m2g |
| q2B1B2 |
|
(3)由于PQ相遇时竖直方向速度相同
即Q球竖直方向下落R时竖直方向分速度为v1
由
| v | 2t |
| v | 20 |
可解得
| B1 |
| B2 |
| 1 |
| 2 |
答:(1)匀强电场的强度为E=
| mg |
| q |
(2)v0的取值范围为v0<(L+
| m2g |
| q2B1B2 |
|
(3)B1:B2=1:2

练习册系列答案
相关题目
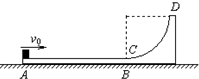 如图所示,竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成,AB恰与圆弧CD在C点相切,轨道固定在水平面上.一个质量为m的小物块(可视为质点)从轨道的A端以初动能Ek0冲上水平轨道AB,沿着轨道运动,由DC弧滑下后停在水平轨道AB的中点.已知水平轨道AB长为L.则( )
如图所示,竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成,AB恰与圆弧CD在C点相切,轨道固定在水平面上.一个质量为m的小物块(可视为质点)从轨道的A端以初动能Ek0冲上水平轨道AB,沿着轨道运动,由DC弧滑下后停在水平轨道AB的中点.已知水平轨道AB长为L.则( )A、小物块与水平轨道的动摩擦因数μ=
| ||
B、为了保证小物块不从轨道的D端离开轨道,圆弧轨道的半径R应满足R≥
| ||
C、如果R=
| ||
D、如果R=
|
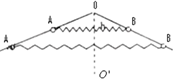 如图所示,竖直平面内两根光滑细杆所构成的角AOB被铅垂线00'平分,∠AOB=120°.两个质量均为m的小环通过水平轻弹簧的作用静止在A、B两处,A、B连线与00'垂直,连线距0点h,已知弹簧原长
如图所示,竖直平面内两根光滑细杆所构成的角AOB被铅垂线00'平分,∠AOB=120°.两个质量均为m的小环通过水平轻弹簧的作用静止在A、B两处,A、B连线与00'垂直,连线距0点h,已知弹簧原长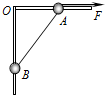 如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,竖直部分光滑,两部分各有质量相等的小球A和B套在杆上,A、B间用不可伸长的轻绳相连,用水平拉力F沿杆向右拉A使之缓慢移动的过程中( )
如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,竖直部分光滑,两部分各有质量相等的小球A和B套在杆上,A、B间用不可伸长的轻绳相连,用水平拉力F沿杆向右拉A使之缓慢移动的过程中( )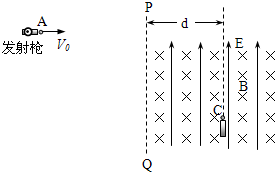 如图所示,竖直平面内,直线PQ右侧足够大的区域内存在竖直向上的匀强电场和垂直于纸面向里的匀强磁场.直线PQ右侧距PQ水平距离为d=28.2cm(计算时取
如图所示,竖直平面内,直线PQ右侧足够大的区域内存在竖直向上的匀强电场和垂直于纸面向里的匀强磁场.直线PQ右侧距PQ水平距离为d=28.2cm(计算时取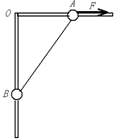 如图所示,竖直平面内放一直角杆,杆的水平部分粗糙,竖直部分光滑,两部分各套有质量分别为mA=2.0kg和mB=1.0kg的小球A和B,A球与水平杆间动摩擦因数μ=0.20,A,B间用不可伸长的轻绳相连,图示位置处OA=1.5m,OB=2.0m,g取10m/s2.(1)若用水平力F沿杆向右拉A,使A由图示位置向右极缓慢地移动0.5m,则该过程中拉力F1作了多少功?
如图所示,竖直平面内放一直角杆,杆的水平部分粗糙,竖直部分光滑,两部分各套有质量分别为mA=2.0kg和mB=1.0kg的小球A和B,A球与水平杆间动摩擦因数μ=0.20,A,B间用不可伸长的轻绳相连,图示位置处OA=1.5m,OB=2.0m,g取10m/s2.(1)若用水平力F沿杆向右拉A,使A由图示位置向右极缓慢地移动0.5m,则该过程中拉力F1作了多少功?