题目内容
8.某光源能发出波长为0.61μm的可见光,用它照射某金属能发生光电效应,产生光电子的最大初动能为0.25eV.已知普朗克常量h=6.63×10-34J.s,光速c=3×108m/s.求:①上述可见光中每个光子的能量;
②该金属的逸出功.
分析 根据E=h$\frac{C}{λ}$ 求出光子的能量,根据光电效应方程求出金属的逸出功.
解答 解:①光子的能量为:E=h$\frac{C}{λ}$=6.63×10-34×$\frac{3×1{0}^{8}}{0.61×1{0}^{-6}}$≈2.07eV.
②根据光电效应方程Ekm=hv-W0得金属的逸出功为:
W0=hv-EKm=2.07-0.25eV=1.82eV.
答:①可见光中每个光子的能量为2.07eV.②金属的逸出功为1.82eV.
点评 该题考查光子的能量以及光电效应方程,解决本题的关键掌握光电效应方程,知道光子能量与波长的关系.

练习册系列答案
相关题目
18. 如图,空军实施投弹训练,A、B两架飞机先后水平飞至P点时释放炸弹,炸弹分别落在水平地面上的a点和b点.忽略空气阻力,则( )
如图,空军实施投弹训练,A、B两架飞机先后水平飞至P点时释放炸弹,炸弹分别落在水平地面上的a点和b点.忽略空气阻力,则( )
 如图,空军实施投弹训练,A、B两架飞机先后水平飞至P点时释放炸弹,炸弹分别落在水平地面上的a点和b点.忽略空气阻力,则( )
如图,空军实施投弹训练,A、B两架飞机先后水平飞至P点时释放炸弹,炸弹分别落在水平地面上的a点和b点.忽略空气阻力,则( )| A. | 飞机A在P点时的飞行速度比飞机B的大 | |
| B. | 两炸弹释放后在空中飞行的时间一样 | |
| C. | 两炸弹释放后在空中飞行的加速度不相等 | |
| D. | 炸弹在空中飞行过程中机械能不守恒 |
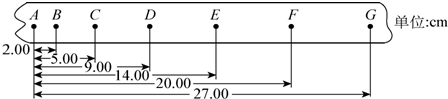
16.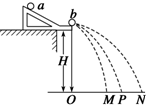 在做“验证动量守恒定律”实验时,入射球a的质量为m1,被碰球b的质量为m2,各小球的落地点如图所示,下列关于这个实验的说法正确的是( )
在做“验证动量守恒定律”实验时,入射球a的质量为m1,被碰球b的质量为m2,各小球的落地点如图所示,下列关于这个实验的说法正确的是( )
 在做“验证动量守恒定律”实验时,入射球a的质量为m1,被碰球b的质量为m2,各小球的落地点如图所示,下列关于这个实验的说法正确的是( )
在做“验证动量守恒定律”实验时,入射球a的质量为m1,被碰球b的质量为m2,各小球的落地点如图所示,下列关于这个实验的说法正确的是( )| A. | 入射球与被碰球最好采用大小相同、质量相等的小球 | |
| B. | 每次都要使入射小球从斜槽上不同的位置滚下 | |
| C. | 要验证的表达式是m1$\overline{ON}$=m1$\overline{OM}$+m2$\overline{OP}$ | |
| D. | 要验证的表达式是m1$\overline{OP}$=m1$\overline{OM}$+m2$\overline{ON}$ |
13. 如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下改变与水平面间的倾角,用以卸下车厢中的货物.假设货物相对于车厢匀加速下滑,则在货物下滑过程中( )
如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下改变与水平面间的倾角,用以卸下车厢中的货物.假设货物相对于车厢匀加速下滑,则在货物下滑过程中( )
 如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下改变与水平面间的倾角,用以卸下车厢中的货物.假设货物相对于车厢匀加速下滑,则在货物下滑过程中( )
如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下改变与水平面间的倾角,用以卸下车厢中的货物.假设货物相对于车厢匀加速下滑,则在货物下滑过程中( )| A. | 地面对货车的支持力逐渐增大 | B. | 地面对货车的支持力逐渐减少 | ||
| C. | 地面对货车的摩擦力方向水平向左 | D. | 地面对货车的摩擦力方向水平向右 |
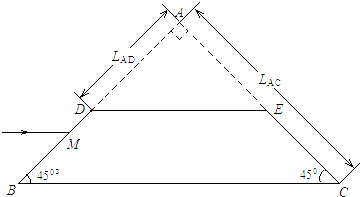
20. 如图所示,两光滑斜面的倾角分别为30°和45°,质量分别为2m和m的两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮的质量和摩擦),分别置于两个斜面上并由静释放;若交换两滑块位置,再由静止释放.则在上述两种情形中正确的有( )
如图所示,两光滑斜面的倾角分别为30°和45°,质量分别为2m和m的两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮的质量和摩擦),分别置于两个斜面上并由静释放;若交换两滑块位置,再由静止释放.则在上述两种情形中正确的有( )
 如图所示,两光滑斜面的倾角分别为30°和45°,质量分别为2m和m的两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮的质量和摩擦),分别置于两个斜面上并由静释放;若交换两滑块位置,再由静止释放.则在上述两种情形中正确的有( )
如图所示,两光滑斜面的倾角分别为30°和45°,质量分别为2m和m的两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮的质量和摩擦),分别置于两个斜面上并由静释放;若交换两滑块位置,再由静止释放.则在上述两种情形中正确的有( )| A. | 质量为2m的滑块受到重力、绳的张力、沿斜面下滑的力和斜面的支持力 | |
| B. | 质量为m的滑块均沿斜面向上运动 | |
| C. | 绳对质量为m的滑块的拉力均大于该滑块对绳的拉力 | |
| D. | 系统在运动中机械能守恒 |