题目内容
17.人造卫星都用太阳能电池供电,现有一个太阳能电池,不接外电路时的电压是600μV,短路电流为30μA,则该电池的电动势为6×10-4V,内阻为20Ω,接20Ω的外电阻时,电流为1.5×10-5A.分析 根据开路电压等于电源电动势,求出电动势;结合短路电流,据闭合电路欧姆定律求出内阻.接20Ω的外电阻时,由闭合电路欧姆定律求电流.
解答 解:由题,电池,不接外电路时的电压是 U=600μV=6×10-4V,则电池的电动势 E=U=6×10-4V
又E=I短r,得内阻 r=$\frac{E}{{I}_{短}}$=$\frac{6×1{0}^{-4}}{3×1{0}^{-5}}$Ω=20Ω
接20Ω的外电阻时,电流为 I=$\frac{E}{R+r}$=$\frac{6×1{0}^{-4}}{20+20}$=1.5×10-5A
故答案为:6×10-4;20;1.5×10-5.
点评 解决本题是明确电池的开路电压等于其电动势,熟练运用闭合电路欧姆定律进行解答.

练习册系列答案
相关题目
7.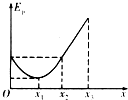 一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位移x变化的关系如图所示,其中O~x2段是对称的曲线,x2~x3是直线段,则下列判断正确的是( )
一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位移x变化的关系如图所示,其中O~x2段是对称的曲线,x2~x3是直线段,则下列判断正确的是( )
 一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位移x变化的关系如图所示,其中O~x2段是对称的曲线,x2~x3是直线段,则下列判断正确的是( )
一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位移x变化的关系如图所示,其中O~x2段是对称的曲线,x2~x3是直线段,则下列判断正确的是( )| A. | x1处电场强度最大 | |
| B. | x2~x3段是匀强电场 | |
| C. | x1、x2、x3处电势φ1、φ2、φ3的关系为φ1>φ2>φ3 | |
| D. | 粒子在O~x2段做匀变速运动,x2~x3段做匀速直线运动 |
5.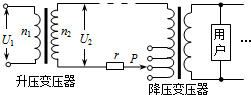 如图所示为某小型电站高压输电示意图.发电机输出功率恒定,升压变压器原、副线圈两端的电压分别为U1和U2.下列说法正确的是( )
如图所示为某小型电站高压输电示意图.发电机输出功率恒定,升压变压器原、副线圈两端的电压分别为U1和U2.下列说法正确的是( )
 如图所示为某小型电站高压输电示意图.发电机输出功率恒定,升压变压器原、副线圈两端的电压分别为U1和U2.下列说法正确的是( )
如图所示为某小型电站高压输电示意图.发电机输出功率恒定,升压变压器原、副线圈两端的电压分别为U1和U2.下列说法正确的是( )| A. | 采用高压输电可以增大输电线中的电流 | |
| B. | 升压变压器原、副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{{U}_{2}}{{U}_{1}}$ | |
| C. | 输电线损耗的功率为$\frac{{{U}_{2}}^{2}}{r}$ | |
| D. | 将P上移,用户获得的电压将升高 |
12. 如图所示,滑块以一定的初速度沿固定光滑斜面向上运动,斜面足够长,已知滑块在第1s内的位移为11.5m,其沿斜面上升的最大高度为9.8m.关于该滑块,下列说法正确的是(重力加速度g取10m/s2)( )
如图所示,滑块以一定的初速度沿固定光滑斜面向上运动,斜面足够长,已知滑块在第1s内的位移为11.5m,其沿斜面上升的最大高度为9.8m.关于该滑块,下列说法正确的是(重力加速度g取10m/s2)( )
 如图所示,滑块以一定的初速度沿固定光滑斜面向上运动,斜面足够长,已知滑块在第1s内的位移为11.5m,其沿斜面上升的最大高度为9.8m.关于该滑块,下列说法正确的是(重力加速度g取10m/s2)( )
如图所示,滑块以一定的初速度沿固定光滑斜面向上运动,斜面足够长,已知滑块在第1s内的位移为11.5m,其沿斜面上升的最大高度为9.8m.关于该滑块,下列说法正确的是(重力加速度g取10m/s2)( )| A. | 滑块的初速度大小为12m/s | B. | 滑块的加速度大小为5m/s2 | ||
| C. | 第3s内的位移大小为1.5m | D. | 前3s内的路程为19.5m |
2.下列说法中正确的是( )
| A. | 物体处于平衡状态时所受的合力一定为零 | |
| B. | 物体所受的合力为零时不一定处于平衡状态 | |
| C. | 物体所受的合力为零时一定处于静止状态 | |
| D. | 物体处于静止状态时合力不一定为零 |
6.一质点在某一木板上做初速度为零的匀加速直线运动,已知质点从木板的前端滑到末端的过程中,它在前3s内的位移与后3s内的位移之比为3:7,后3s内的位移比前3s内的位移多24m,取g=10m/s2.则( )
| A. | 该质点总共运动了6s | |
| B. | 该质点的加速度大小为2m/s2 | |
| C. | 木板的长度为50m | |
| D. | 质点在木板上运动的末速度大小为18m/s |
7.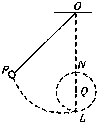 如图所示,一长为R的细绳的上端固定在天花板上靠近墙壁的O点,下端拴一小球,L点是小球下垂时的平衡位置,Q点代表一固定在墙上的细长钉子,位于OL直线上,N点在Q点正上方,且QN=QL=$\frac{R}{4}$.现将小球从竖直位置(保持绳绷直)拉开到P点,绳子与竖直夹角cosα=$\frac{1}{8}$释放后任其向L摆动,运动过程中一切阻力略不计,小球到达L后.因细绳被长钉挡住,将开始沿以Q为中心的圆弧继续运动,在此以后( )
如图所示,一长为R的细绳的上端固定在天花板上靠近墙壁的O点,下端拴一小球,L点是小球下垂时的平衡位置,Q点代表一固定在墙上的细长钉子,位于OL直线上,N点在Q点正上方,且QN=QL=$\frac{R}{4}$.现将小球从竖直位置(保持绳绷直)拉开到P点,绳子与竖直夹角cosα=$\frac{1}{8}$释放后任其向L摆动,运动过程中一切阻力略不计,小球到达L后.因细绳被长钉挡住,将开始沿以Q为中心的圆弧继续运动,在此以后( )
 如图所示,一长为R的细绳的上端固定在天花板上靠近墙壁的O点,下端拴一小球,L点是小球下垂时的平衡位置,Q点代表一固定在墙上的细长钉子,位于OL直线上,N点在Q点正上方,且QN=QL=$\frac{R}{4}$.现将小球从竖直位置(保持绳绷直)拉开到P点,绳子与竖直夹角cosα=$\frac{1}{8}$释放后任其向L摆动,运动过程中一切阻力略不计,小球到达L后.因细绳被长钉挡住,将开始沿以Q为中心的圆弧继续运动,在此以后( )
如图所示,一长为R的细绳的上端固定在天花板上靠近墙壁的O点,下端拴一小球,L点是小球下垂时的平衡位置,Q点代表一固定在墙上的细长钉子,位于OL直线上,N点在Q点正上方,且QN=QL=$\frac{R}{4}$.现将小球从竖直位置(保持绳绷直)拉开到P点,绳子与竖直夹角cosα=$\frac{1}{8}$释放后任其向L摆动,运动过程中一切阻力略不计,小球到达L后.因细绳被长钉挡住,将开始沿以Q为中心的圆弧继续运动,在此以后( )| A. | 小球运动到L点速度为$\frac{\sqrt{5gR}}{2}$ | |
| B. | 小球未运动到N点就掉下来了 | |
| C. | 小球通过N点的速度为$\frac{\sqrt{gR}}{2}$ | |
| D. | 小球在竖直面将绕Q点已知做圆周运动,直到球撞到钉子为止 |