题目内容
【题目】如图所示,一细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处,细线的另一端拴一质量为m的小球,重力加速度为g。当滑块以加速度a在水平面上做匀加速运动时,小球的受力情况和滑块A的加速度a的大小关系正确的是( )
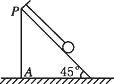
A. 若绳对小球恰好没有拉力,则滑块A一定有向右的加速度,且a=g
B. 若绳对小球恰好没有拉力,则滑块A一定有向左的加速度,且a=g
C. 若滑块A向左以a=g做匀加速运动时,绳对小球的拉力为![]()
D. 若滑块A向左以a=g做匀加速运动时,绳对小球的拉力为![]()
【答案】AC
【解析】
根据牛顿第二定律求出拉力为零时小球的加速度,当滑块A向左以a=g做匀加速运动时小球恰好没有脱离斜面飘起,再根据求解第二定律列式求解拉力的大小;
A、若绳对小球恰好没有拉力,则对小球进行受力分析如图所示:
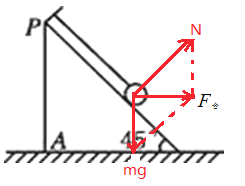
根据牛顿第二定律可知:![]() ,则
,则![]() ,方向水平向右,故选项A正确,B错误;
,方向水平向右,故选项A正确,B错误;
C、当滑块A向左以a=g做匀加速运动时,则小球的合力为:![]() ,方向水平向左,则对小球进行受力分析如图所示:
,方向水平向左,则对小球进行受力分析如图所示:

则此时小球与斜面之间恰好没有弹力,则由图可知绳的拉力为:![]() ,故选项C正确,D错误。
,故选项C正确,D错误。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目