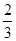Question

如图所示，两平行导轨间距L＝0.1 m，足够长光滑的倾斜部分和粗糙的水平部分圆滑连接，倾斜部分与水平面的夹角θ＝30°，垂直斜面方向向上的磁场磁感应强度B＝0.5 T，水平部分没有磁场．金属棒ab质量m＝0.005 kg、电阻r＝0.02 Ω，运动中与导轨始终接触良好，并且垂直于导轨．电阻R＝0.08 Ω，其余电阻不计．当金属棒从斜面上离地高h＝1.0 m以上的任何地方由静止释放后，在水平面上滑行的最大距离x都是1.25 m．取g＝10 m/s²，求：

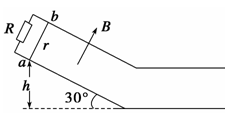
(1)金属棒在斜面上的最大速度；
(2)金属棒与水平面间的动摩擦因数；
(3)从高度h＝1.0 m处滑下后电阻R上产生的热量．

Answer 1

（1）1.0 m/s；（2）0.04  ；（3）3.8×10^－2 J

试题分析：(1)到达水平面之前已经开始匀速运动，设最大速度为v，感应电动势E＝BLv      
感应电流I＝                                                  
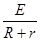
安培力F＝BIL                                                   
匀速运动时，mgsin θ＝F                                            
解得v＝1.0 m/s                                                 
(2)滑动摩擦力f＝μmg                                              
金属棒在摩擦力作用下做匀减速直线运动，有f＝ma                      
金属棒在水平面做匀减速直线运动，有v²＝2ax                          
解得μ＝0.04        (用动能定理同样可以得分)
(3)下滑的过程中，由动能定理可得：
mgh－W＝mv²                                                                                                
安培力所做的功等于电路中产生的焦耳热W＝Q                       
电阻R上产生的热量：Q_R＝Q                                    
联立解得：Q_R＝3.8×10^－2 J