ЬтФПФкШн
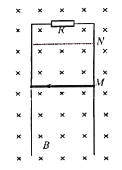
ЁОЬтФПЁПШчЭМЫљЪОЃЌвЛЪњжБУцФкЕФЙьЕРгЩДжВкаБУцABКЭАыОЖЮЊRЕФЙтЛЌдВЙьЕРBCDзщГЩЃЌABгыBCDЯрЧагкBЕуЃЌCЮЊдВЙьЕРЕФзюЕЭЕуЃЌдВЛЁBCЫљЖдгІЕФдВаФНЧІШЃН60ЁуЁЃЯжгавЛжЪСПЮЊmЕФЮяПщЃЈПЩЪгЮЊжЪЕуЃЉДгЙьЕРABCЩЯРыЕиУцФГвЛИпЖШhЃЈДѓаЁПЩБфЃЉДІгЩОВжЙЯТЛЌЃЌвбжЊЮяПщгыаБУцМфЕФЖЏФІВСвђЪ§ЮЊІЬЃН![]() ЃЌжиСІМгЫйЖШгУgБэЪОЃЌЧѓЃК
ЃЌжиСІМгЫйЖШгУgБэЪОЃЌЧѓЃК
(1)ЕБhЃН![]() RЪБЃЌЮяПщЛЌЕНCЕуЪБЖдЙьЕРЕФбЙСІFNЃЛ
RЪБЃЌЮяПщЛЌЕНCЕуЪБЖдЙьЕРЕФбЙСІFNЃЛ
(2)ЕБhЮЊЖрЩйЪБЃЌЮяПщЧЁФмЛЌЕНдВЙьЕРЕФзюИпЕуDЁЃ

ЁОД№АИЁП(1)3mgЃЛ(2)![]() R
R
ЁОНтЮіЁП
(1)Й§BЕузївЛЬѕЫЎЦНЕФИЈжњЯпЃЌгыЭМжаAGКЭOCЗжБ№НЛгкEКЭFСНЕуЃЌ

гЩМИКЮЙиЯЕвзЕУ
ЁЯEABЃНЁЯOBFЃН30Ёу
![]()
![]()
дђ
![]()
![]()
![]()
ДгAЕНCЙ§ГЬЃЌИљОнЖЏФмЖЈРэ
![]()
гжга
![]()
НтЕУ
![]()
ИљОнХЃЖйЕкШ§ЖЈТЩПЩжЊЃЌбЙСІЮЊ3mgЁЃ
(2)ДгAЕНDЙ§ГЬЃЌИљОнЖЏФмЖЈРэ
![]()
гжга
![]()
НтЕУ
![]()

СЗЯАВсЯЕСаД№АИ
 ЪюМйзївЕКЃбрГіАцЩчЯЕСаД№АИ
ЪюМйзївЕКЃбрГіАцЩчЯЕСаД№АИ БОЭСНЬИЈгЎдкЪюМйИпаЇМйЦкзмИДЯАдЦФЯПЦММГіАцЩчЯЕСаД№АИ
БОЭСНЬИЈгЎдкЪюМйИпаЇМйЦкзмИДЯАдЦФЯПЦММГіАцЩчЯЕСаД№АИ ЪюМйзївЕББОЉвеЪѕгыПЦбЇЕчзгГіАцЩчЯЕСаД№АИ
ЪюМйзївЕББОЉвеЪѕгыПЦбЇЕчзгГіАцЩчЯЕСаД№АИ
ЯрЙиЬтФП