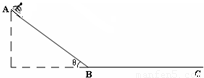
题目内容
某一旅游景区,建有一山坡滑草运动场.该山坡可看成有一定倾角的斜面,一名游客与滑草装置总质量m=80kg,他从静止开始匀加速下滑,t=5s时滑至底端.已知斜面和水平面动摩擦因数相同,游客在整个运动过程中速率v与时间t的关系如图所示(不计空气阻力,g取10m/s2,)求:(1)滑草装置与草皮间的动摩擦因数μ;
(2)斜面的倾角θ;
(3)通过计算证明游客从顶端滑至底端的过程满足动能定理.
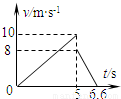
【答案】分析:(1)由速度与时间图象可知,加速度大小,从而由μmg=ma,可求出动摩擦因数;
(2)由游客和滑草装置整体在斜面上作匀加速运动,由牛顿第二定律结合sin2θ+cos2θ=1,可求出斜面的倾角;
(3)运用功的表达式,求出游客在此过程中总功,再由动能表达式求出动能的增量,最后进行比较,从而确定是否满足动能定理.
解答:解:(1)游客和滑草装置整体在水平草皮上作匀减速运动时,由v-t图加速度大小为:
a1=5m/s2=μg,
μ=0.5
(2)游客和滑草装置整体在斜面上作匀加速运动时,由:gsinθ-μgcosθ=2m/s2,
结合sin2θ+cos2θ=1,
则sinθ=0.6,即θ=37°;
(3)游客在此过程中,
重力做功:WG=mgxsinθ=80×10×25×0.6=12000J,
斜面的摩擦力做功:Wf=-μmgxcosθ=-8000 J,
动能的增量△EK=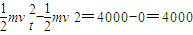 J
J
则合外力的功W合=WG+Wf=4000 J,
W合=△EK即可证明.
答:(1)滑草装置与草皮间的动摩擦因数μ为0.5;
(2)斜面的倾角θ等于37°;
(3)W合=△EK即可证明,游客从顶端滑至底端的过程满足动能定理.
点评:考查由运动情况来确定受力情况,并运用功与动能的表达式来证明动能定理的正确性.本题有个亮点就是运用sin2θ+cos2θ=1来求出倾角.
(2)由游客和滑草装置整体在斜面上作匀加速运动,由牛顿第二定律结合sin2θ+cos2θ=1,可求出斜面的倾角;
(3)运用功的表达式,求出游客在此过程中总功,再由动能表达式求出动能的增量,最后进行比较,从而确定是否满足动能定理.
解答:解:(1)游客和滑草装置整体在水平草皮上作匀减速运动时,由v-t图加速度大小为:
a1=5m/s2=μg,
μ=0.5
(2)游客和滑草装置整体在斜面上作匀加速运动时,由:gsinθ-μgcosθ=2m/s2,
结合sin2θ+cos2θ=1,
则sinθ=0.6,即θ=37°;
(3)游客在此过程中,
重力做功:WG=mgxsinθ=80×10×25×0.6=12000J,
斜面的摩擦力做功:Wf=-μmgxcosθ=-8000 J,
动能的增量△EK=
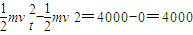 J
J则合外力的功W合=WG+Wf=4000 J,
W合=△EK即可证明.
答:(1)滑草装置与草皮间的动摩擦因数μ为0.5;
(2)斜面的倾角θ等于37°;
(3)W合=△EK即可证明,游客从顶端滑至底端的过程满足动能定理.
点评:考查由运动情况来确定受力情况,并运用功与动能的表达式来证明动能定理的正确性.本题有个亮点就是运用sin2θ+cos2θ=1来求出倾角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在某一旅游景区,建有一山坡滑雪运动项目.某段斜坡可看成倾角θ=30°的斜面,一名滑雪者总质量m=80kg,他在这段斜坡上从静止开始匀加速下滑50m时,其速度增大到20m/s,(不计空气阻力,取g=10m/s2)问:
在某一旅游景区,建有一山坡滑雪运动项目.某段斜坡可看成倾角θ=30°的斜面,一名滑雪者总质量m=80kg,他在这段斜坡上从静止开始匀加速下滑50m时,其速度增大到20m/s,(不计空气阻力,取g=10m/s2)问: 某一旅游景区,建有一山坡滑草运动场.该山坡可看成有一定倾角的斜面,一名游客与滑草装置总质量m=80kg,他从静止开始匀加速下滑,t=5s时滑至底端.已知斜面和水平面动摩擦因数相同,游客在整个运动过程中速率v与时间t的关系如图所示(不计空气阻力,g取10m/s2,)求:
某一旅游景区,建有一山坡滑草运动场.该山坡可看成有一定倾角的斜面,一名游客与滑草装置总质量m=80kg,他从静止开始匀加速下滑,t=5s时滑至底端.已知斜面和水平面动摩擦因数相同,游客在整个运动过程中速率v与时间t的关系如图所示(不计空气阻力,g取10m/s2,)求: