题目内容
 在某一旅游景区,建有一山坡滑雪运动项目.某段斜坡可看成倾角θ=30°的斜面,一名滑雪者总质量m=80kg,他在这段斜坡上从静止开始匀加速下滑50m时,其速度增大到20m/s,(不计空气阻力,取g=10m/s2)问:
在某一旅游景区,建有一山坡滑雪运动项目.某段斜坡可看成倾角θ=30°的斜面,一名滑雪者总质量m=80kg,他在这段斜坡上从静止开始匀加速下滑50m时,其速度增大到20m/s,(不计空气阻力,取g=10m/s2)问:(1)滑雪者在下滑过程中受到的摩擦力f为多大?
(2)滑板与雪地之间的动摩擦因数μ为多大?
分析:(1)根据匀变速直线运动的位移时间公式求出下滑的加速度,对物体进行受力分析,根据牛顿第二定律求出下滑过程中的摩擦力.
(2)在垂直斜面方向上,受力平衡,求出正压力,根据滑动摩擦力的公式即可求得动摩擦力因素.
(2)在垂直斜面方向上,受力平衡,求出正压力,根据滑动摩擦力的公式即可求得动摩擦力因素.
解答:解:(1)以滑雪者为研究对象,其受力情况如图所示,受到重力G=mg,斜坡的支持力N和摩擦力f.
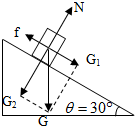
将重力G沿斜面和垂直斜面方向分解为G1和G2.
由几何知识得:
G1=mgsinθ
G2=mgcosθ
设下滑的加速度为a,由公式
-
=2as可得:
a=
=
m/s2=4m/s2
由牛顿第二定律得:F合=ma=80×4N=320N
由受力分析图可知:F合=G1-f=mgsinθ-f
联立解得:f=80N
(2)斜面的支持力 N=G2=mgcosθ
滑动摩擦力公式 f=μN
两式联立解得:μ=0.12
答:(1)滑雪者在下滑过程中受到的摩擦力f为80N;
(2)滑板与雪地之间的动摩擦因数μ为0.12.

将重力G沿斜面和垂直斜面方向分解为G1和G2.
由几何知识得:
G1=mgsinθ
G2=mgcosθ
设下滑的加速度为a,由公式
| v | 2 t |
| v | 2 0 |
a=
| ||||
| 2s |
| 202-0 |
| 2×50 |
由牛顿第二定律得:F合=ma=80×4N=320N
由受力分析图可知:F合=G1-f=mgsinθ-f
联立解得:f=80N
(2)斜面的支持力 N=G2=mgcosθ
滑动摩擦力公式 f=μN
两式联立解得:μ=0.12
答:(1)滑雪者在下滑过程中受到的摩擦力f为80N;
(2)滑板与雪地之间的动摩擦因数μ为0.12.
点评:解决本题的关键知道加速度是联系力学和运动学的桥梁,通过加速度可以根据力求运动,也可以根据运动求力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在某一旅游景区,建有一山坡滑草运动项目.设山坡AB可看成长度为L=50m、倾角θ=37°的斜面,山坡低端与一段水平缓冲段BC圆滑连接.一名游客连同滑草装置总质量m=80kg,滑草装置与AB段及BC段间动摩擦因数均为?=0.25.他从A处由静止开始匀加速下滑,通过B点滑入水平缓冲段. 不计空气阻力,取g=10m/s2,sin37°≈0.6.结果保留2位有效数字.求:
在某一旅游景区,建有一山坡滑草运动项目.设山坡AB可看成长度为L=50m、倾角θ=37°的斜面,山坡低端与一段水平缓冲段BC圆滑连接.一名游客连同滑草装置总质量m=80kg,滑草装置与AB段及BC段间动摩擦因数均为?=0.25.他从A处由静止开始匀加速下滑,通过B点滑入水平缓冲段. 不计空气阻力,取g=10m/s2,sin37°≈0.6.结果保留2位有效数字.求: