题目内容
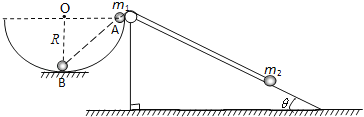
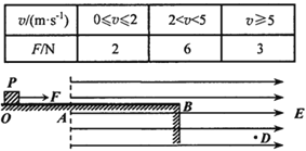
【题目】如图所示,粗糙、绝缘的直轨道OB固定在水平桌面上,B端与桌面边缘对齐,A是轨道上一点,过A点并垂直于轨道的竖直面右侧有大小E=1.5×106N/C,方向水平向右的匀强电场。带负电的小物体P电荷量是2.0×10-6C,质量m=0.25kg,与轨道间动摩擦因数μ=0.4,P从O点由静止开始向右运动,经过0.55s到达A点,到达B点时速度是5m/s,到达空间D点时速度与竖直方向的夹角为α,且tanα=1.2。P在整个运动过程中始终受到水平向右的某外力F作用,F大小与P的速率v的关系如表所示。P视为质点,电荷量保持不变,忽略空气阻力,取g=10 m/s2,求:
(1)小物体P从开始运动至速率为2m/s所用的时间;
(2)小物体P从A运动至D的过程,电场力做的功。
【答案】(1)t1=0.5s;(2)
【解析】试题分析:(1)小物体P做匀加速直线运动,根据牛顿第二定律计算加速度的大小,根据速度公式计算受到的大小;
(2)根据物体的运动的不同的过程,逐项计算受到和位移的大小,在利用功的公式来计算电场力做的功;
解:(1)小物体P的速率从0只2m/s,受外力F1=2N,设其做匀变速直线运动的加速度为a1,经过时间△t1,则
F1﹣μmg=ma1①
v1=a1△t ②
由式代入数据得△t1=0.5s ③
(2)小物体P从2m/s运动至A点,受外力F2=6N,设其做匀变速直线运动的加速度为a2,则
F2﹣μmg=ma2④
设小物体P从速度v1经过△t2时间,在A点的速度为v2,则
△t2=0.55s﹣△t1⑤
v2=v1+a2△t2⑥
P从A点至B点,受外力F2=6N、电场力和滑动摩擦力的作用,
设其做匀变速直线运动的加速度为a3,电荷量为q,在B点的速度为v3,从A点至B点的位移为x1,则有:
F2﹣μmg﹣qE=ma3⑦
![]() ⑧
⑧
P以速度v3滑出轨道右端B点,设水平方向外力为F3,电场力大小为FE,
有FE=F3⑨
F3与FE大小相等方向相反,P水平方向所受合力为零,所以P从B点开始做初速度为v3的平抛运动.
设P从B点运动至D点用是为△t3,水平位移为x2,
由题意知![]() (10)
(10)
x2=v3△t3(11)
设小物体P从A点至D点电场力做功为W,则有:
W=﹣qE(x1+x2) (12)
联立④⑧(10)(12)式并代入数据得W=﹣9.25J.
答:
(1)小物体P从开始运动至速率为2m/s所用的时间为0.5s;
(2)小物体P从A运动至D的过程,电场力做的功为﹣9.25J.