��Ŀ����
����Ŀ����̽������ļ��ٶ���������Ĺ�ϵʵ���У�
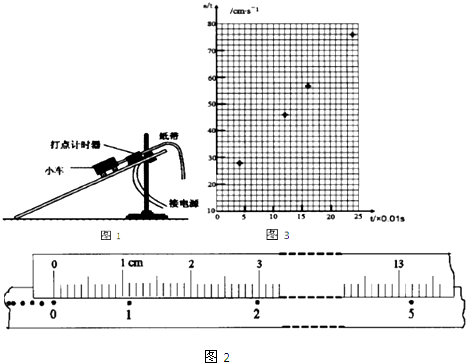
��ͬѧ����ͼ��װ�ã�����С��(����������)������M���䣬ϸ���¶����ҹ����������mg��ΪС���ܵ��ĺ���F���ô���ʱ�����С���˶��ļ��ٶ�a��

(1)����ʵ�����������˵����ȷ����____________
A��ʵ��ǰӦ���ڻ��ָ߶ȣ�ʹ���ֺ�С�����ϸ����ľ��ƽ��
B��ƽ��Ħ����ʱ����ϸ�ߵ��¶����ҹ��룬ʹС�����ߵ������������������»�
C��ÿ�θı�С�����ܵ�������Ҫ����ƽ��Ħ����
D��ʵ��ʱӦ���ͷ�С�������ͨ����ʱ����Դ
(2)ͼ��Ϊʵ���д��ֽ����һ���֣��ӱȽ������ĵ㼣����ֽ���ϱ��������5��������A��B��C��D��E����������������ʱ����ΪT��������������ľ���x1��x2��x3��x4����ͬѧ�����õ�С�����ٶȵı���ʽa��________��
(3)�ı�ϸ���¶˹���ĸ������õ�a��Fͼ����ͼ����ʾ�����ͼ���϶���������Ҫԭ����____
A��ƽ��Ħ�������� B��ƽ��Ħ��������
C��û������M>>m������ D��������߲���ȷ
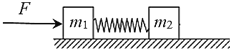
��ͬѧ���ò����Ʋ�ϸ��������Ϊ��������������ͼʵ��װ�ã�װ�ж����ֵij�ľ��̶���ˮƽʵ��̨�ϣ����Ҷ˹̶�һ�����ֵĻ������С��������͵��ɲ�����ͨ�����ڻ����ϵ������������ſ����룬�����ڳ�ľ�������ȼ���ֱ���˶���
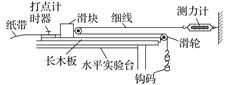
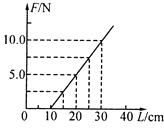
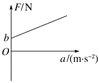
(4)�������ɲ����Ƶ�ʾ��F������ֽ�����õ������˶��ļ��ٶ�a���ı乳��������ظ�ʵ�顣�Ե��ɲ����Ƶ�ʾ��FΪ�����꣬�Լ��ٶ�aΪ�����꣬�õ���ͼ��������ؾ�Ϊb��б��Ϊk��һ����бֱ�ߣ���ͼ��ʾ����֪�������ٶ�Ϊg�����Ի�������֮���Ħ�����������������ɼ���������ľ��֮��Ķ�Ħ����������________��������뻬��̶��Ķ����ֵ�������M=________��Ҫ��(4)���������վ���b��k��g�е���ĸ��ʾ����
���𰸡� A ![]() C
C ![]() 2k
2k
����������1�����ڻ��ֵĸ߶ȣ�ʹǣ��ľ���ϸ���볤ľ�屣��ƽ�У���������������ں�������A��ȷ���ڵ���ģ����б��ƽ��ľ���ܵ��Ļ���Ħ����ʱ����Ӧ���ҹ��룬��B��������ƽ��Ħ����֮����Mgsin��=��Mgcos������tan��=������������С���������Ƿ�ı䣬С�����ܵĻ���Ħ����������С����������б��ķ������ı�С���������ı���С������������Ҫ����ƽ��Ħ��������C����ʵ�鿪ʼʱ�Ƚ�ͨ����ʱ���ĵ�Դ����ƽ�ȹ��������ͷ�ľ�飬��D��������ѡA.
��2����֪����ʱ����ԴƵ��Ϊ50Hz����ֽ�������ڼ�������ʱ����ΪT=5��0.02s=0.1s��
������x=aT2�ɵã�xCE-xAC=a��2T��2��С���˶��ļ��ٶ�Ϊa=![]() ��
��
��3��������F�����������ҹ�������m������������M����m����������ϲ�����������������ѡC��
��4�������ܵ�������TΪ���ɳ�ʾ��������������T=2F
�����ܵ���Ħ����Ϊ��f=��Mg
��ţ�ٵڶ����ɿɵã�T-f=Ma
�����F����ٶ�a�ĺ�����ϵʽΪ�� ![]()
��ͼ��������Ϣ�ɵ�ͼ��ؾ�Ϊ��b= ![]() ����ͼ��б��Ϊk=
����ͼ��б��Ϊk=![]()
��ã�M=2k����=![]() ��
��

 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�