题目内容
如图所示，在光滑水平面上有两相同的木板B和C。物块A（视为质点）位于B的右端，Ａ、B、C的质量相等。现A和B以同一速度滑向静止的C，B与C发生正碰且碰后B和C粘在一起运动，A在C上滑行，A与C间有摩擦。已知Ａ滑到Ｃ的右端而未掉下，试问：B、C发生正碰到A刚移动到C右端期间，C所走过的距离是C板长度的多少倍？
倍设Ａ、B、C的质量均为m，碰前A与B速度为v0，碰后B与C的共同速度为v1，对B与C由动量守恒定律得mv0＝2mv1（2分）
设A滑至C的右端时，三者共同速度为v2，对Ａ、B、C由动量守恒定律得2mv0＝3mv2（2分）
设A与C间摩擦力为f，从发生碰撞到A运动至C的右端时，C的位移为x，由动能定理
f x＝
·2mv22－·2mv12（2分）
－f (x＋l)＝mv22－mv02（2分）
由以上各式解得x∶l＝7∶3（2分）
设A滑至C的右端时，三者共同速度为v2，对Ａ、B、C由动量守恒定律得2mv0＝3mv2（2分）
设A与C间摩擦力为f，从发生碰撞到A运动至C的右端时，C的位移为x，由动能定理
f x＝
·2mv22－·2mv12（2分）－f (x＋l)＝
mv22－mv02（2分）由以上各式解得x∶l＝7∶3（2分）
练习册系列答案
相关题目
；得出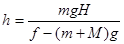
。
①小球C与劈A分离时，A的速度；
、
，开始时B、C均静止，A以初速度v0向右运动，A与B相撞后分开，B又与C发生碰撞并粘在一起，此后A与B间的距离保持不变。求B与C碰撞前B的速度大小。
，第一次刚至O点时速度为
，随后滑上滑槽A，A、B分离．求：