题目内容
【题目】如图甲所示，斜面倾角为37°，一宽为l＝0.43 m的有界匀强磁场垂直于斜面向上，磁场边界与斜面底边平行．在斜面上由静止释放一正方形金属线框，线框沿斜面下滑，下边与磁场边界保持平行．取斜面底边重力势能为零，从线框开始运动到恰好完全进入磁场的过程中，线框的机械能E和位移s之间的关系如图乙所示，图中①、②均为直线段．已知线框的质量为m＝0.1 kg，电阻为R＝0.06 Ω，重力加速度取g＝10 m/s2.求：
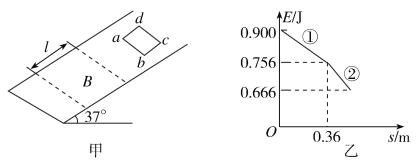
(1)金属线框与斜面间的动摩擦因数；
(2)金属线框刚进入磁场到恰完全进入磁场所用的时间；
(3)金属线框穿越磁场的过程中，线框中产生的最大电功率(本小题保留两位有效数字)．
【答案】(1)0.5 (2)0.125 s (3)0.43 W
【解析】(1)减少的机械能等于克服摩擦力所做的功ΔE1＝Wf1
而ΔE1＝0.900 J－0.756 J＝0.144 J
Wf1＝μmgcos37s1
其中s1＝0.36 m
解得μ＝0.5
(2)金属线框进入磁场的过程中，减小的机械能等于克服摩擦力和安培力所做的功，机械能仍均匀减小，因此安培力也为恒力，线框做匀速运动v
＝2as1
其中a＝gsin37°－μgcos37°＝2 m/s2
可解得线框刚进磁场时的速度大小为v1＝1.2 m/s
ΔE2＝Wf2＋WA＝(f＋FA)s2
其中ΔE2＝0.756 J－0.666 J＝0.09 J
f＋FA＝mgsin37°＝0.6 N
s2为线框的侧边长
即线框进入磁场过程运动的距离，可求出
s2＝0.15 m t＝
＝0.125 s
(3)线框刚出磁场时速度最大，线框内的电功率最大
Pm＝I2R＝
由v＝v＋2a(l－s2)
可求得v2＝1.6 m/s
根据线框匀速进入磁场时，FA＋μmgcos37°＝mgsin37°
可求出FA＝0.2 N
又因为FA＝BIL＝
可求出B2L2＝0.01
代入数据解得Pm＝I2R＝
＝0.43 W
