题目内容
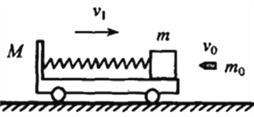
【题目】如图所示，光滑水平面上有一质量M=1.0kg的小车，小车右端有一个质量m=0.90kg的滑块，滑块与小车左端的挡板之间用轻弹簧相连接，滑块与车面间的动摩擦因数μ=0.20，车和滑块一起以v1=10m/s的速度向右做匀速直线运动，此时弹簧为原长．一质量m0=0.10kg的子弹，以v0=50m/s的速度水平向左射入滑块而没有穿出，子弹射入滑块的时间极短．当弹簧压缩到最短时，弹簧被锁定(弹簧在弹性限度内)，测得此时弹簧的压缩量d=0.50m，（ g=10m/s2，√7=2.65），求：
(1)子弹与滑块刚好相对静止的瞬间，子弹与滑块共同速度的大小和方向；
(2)弹簧压缩到最短时，小车的速度大小和弹簧的弹性势能；
(3)如果当弹簧压缩到最短时，不锁定弹簧，则弹簧再次回到原长时，车的速度大小．
【答案】（1）4m/s ；与车方向相同；（2）7m/s；8J（3）4.35J
【解析】（1）设相对静止时共同速度为v，根据动量守恒定律
mv1+m0v0=（m0+m）v
解得：v=4m/s，方向与车方向相同向右．
（2）设弹簧压缩到最短时它们的共同速度为v′，根据动量守恒定律
Mv1+（m+m0）v=（M+m+m0）v′
解得：v′=7m/s，
设滑块与车摩擦产生的热为Q，弹簧的最大弹性势能为EP，根据能量守恒有：
Mv12+
（m+m0）v2=
（M+m+m0）v′2+Q+Ep，
Q=μ（m+m）gd=1J，
解得：Ep=8J．
（3）设弹簧再次回到原长时，车的速度为v1，滑块（和子弹）的速度为v2，根据动量守恒定律
（M+m+m0）v′=Mv1+（m+m0）v2，
根据能量守恒： 
（M+m0+m）v′2+Ep=
Mv12+
（m0+m）v22+Q，
解得：车的速度大小为v1=（7-
）m/s=4.35m/s，
（另一解v1=（7+
）m/s舍去）．
