题目内容
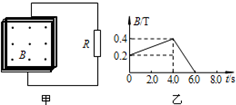 如图甲所示,在一个正方形金属线圈区域内,存在着磁感应强度B随时间变化的匀强磁场,磁场的方向与线圈平面垂直.金属线圈所围的面积S=200cm2,匝数n=1000,线圈电阻r=1.0Ω.线圈与电阻R构成闭合回路,电阻R=4.0Ω.匀强磁场的磁感应强度随时间变化的情况如图乙所示,求:
如图甲所示,在一个正方形金属线圈区域内,存在着磁感应强度B随时间变化的匀强磁场,磁场的方向与线圈平面垂直.金属线圈所围的面积S=200cm2,匝数n=1000,线圈电阻r=1.0Ω.线圈与电阻R构成闭合回路,电阻R=4.0Ω.匀强磁场的磁感应强度随时间变化的情况如图乙所示,求:(1)在t=2.0s时刻,通过电阻R的感应电流的大小;
(2)在t=2.0s时刻,电阻R消耗的电功率;
(3)0~6.0s内整个闭合电路中产生的热量.
分析:(1)由图读出磁通量的变化率,根据法拉第电磁感应定律求出感应电动势,由欧姆定律求解感应电流的大小.
(2)由P=I2R求出电阻R消耗的电功率.
(3)根据焦耳定律分别求出0~4.0s时间内和4.0s~6.0s时间内的热量,再求总和.
(2)由P=I2R求出电阻R消耗的电功率.
(3)根据焦耳定律分别求出0~4.0s时间内和4.0s~6.0s时间内的热量,再求总和.
解答:解:(1)根据法拉第电磁感应定律,0~4.0s时间内线圈中磁通量均匀变化,产生恒定的感应电流.
t1=2.0s时的感应电动势E1=n
=n
根据闭合电路欧姆定律,闭合回路中的感应电流I1=
解得 I1=0.2A
(2)在t=2.0s时刻,电阻R消耗的电功率P=I12R=0.16W.
(3)根据焦耳定律,0~4.0s内闭合电路中产生的热量
Q1=I12(r+R)△t1=0.8 J
由图象可知,在4.0s~6.0s时间内,线圈中产生的感应电动势E2=n
=n
根据闭合电路欧姆定律,t2=5.0s时闭合回路中的感应电流I2=
=0.8A
闭合电路中产生的热量 Q2=I22(r+R)△t2=6.4J
故0~6.0s内整个闭合电路中产生的热量Q=Q1+Q2=7.2J.
答:(1)在t=2.0s时刻,通过电阻R的感应电流的大小为0.2A;
(2)在t=2.0s时刻,电阻R消耗的电功率为0.16W;
(3)0~6.0s内整个闭合电路中产生的热量为7.2J.
t1=2.0s时的感应电动势E1=n
| △Φ |
| △t1 |
| (B4-B0)S |
| △t1 |
根据闭合电路欧姆定律,闭合回路中的感应电流I1=
| E1 |
| R+r |
解得 I1=0.2A
(2)在t=2.0s时刻,电阻R消耗的电功率P=I12R=0.16W.
(3)根据焦耳定律,0~4.0s内闭合电路中产生的热量
Q1=I12(r+R)△t1=0.8 J
由图象可知,在4.0s~6.0s时间内,线圈中产生的感应电动势E2=n
| △Φ2 |
| △t2 |
| Φ6-Φ4 |
| △t2 |
根据闭合电路欧姆定律,t2=5.0s时闭合回路中的感应电流I2=
| E2 |
| R+r |
闭合电路中产生的热量 Q2=I22(r+R)△t2=6.4J
故0~6.0s内整个闭合电路中产生的热量Q=Q1+Q2=7.2J.
答:(1)在t=2.0s时刻,通过电阻R的感应电流的大小为0.2A;
(2)在t=2.0s时刻,电阻R消耗的电功率为0.16W;
(3)0~6.0s内整个闭合电路中产生的热量为7.2J.
点评:本题是电磁感应与电路知识简单的综合.当穿过回路的磁通量均匀变化时,回路中产生恒定电流,可以用焦耳定律求解热量.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图甲所示,在同一竖直平面内有两正对着的相同半圆光滑轨道,它们相隔一定的距离,虚线沿竖直方向,一小球能在期间运动.今在最高点A与最低点B各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来.当两半圆轨道间距变化时,测得A,B两点压力差△F与距离x的图象如图乙所示,g取10m/s2,不计空气阻力,求:
如图甲所示,在同一竖直平面内有两正对着的相同半圆光滑轨道,它们相隔一定的距离,虚线沿竖直方向,一小球能在期间运动.今在最高点A与最低点B各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来.当两半圆轨道间距变化时,测得A,B两点压力差△F与距离x的图象如图乙所示,g取10m/s2,不计空气阻力,求:
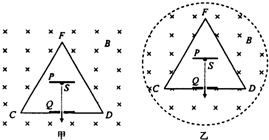 如图甲所示,在空心三棱柱CDF以外足够大的空间中,充满着磁感应强度为B的匀强磁场.三棱柱的轴线与磁场平行,截面边长为L,三棱柱用绝缘薄板材料制成,其内部有平行于CD侧面的金属板P、Q,两金属板间的距离为d,P板带正电,Q板带负电,Q板中心有一小孔,P板上与小孔正对的位置有一个粒子源S,从S处可以发出初速度为0、带电量为+q、质量为m的粒子,这些粒子与三棱柱侧面碰撞时无能量损失.试求:
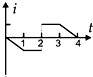
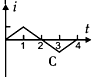
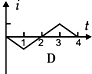
如图甲所示,在空心三棱柱CDF以外足够大的空间中,充满着磁感应强度为B的匀强磁场.三棱柱的轴线与磁场平行,截面边长为L,三棱柱用绝缘薄板材料制成,其内部有平行于CD侧面的金属板P、Q,两金属板间的距离为d,P板带正电,Q板带负电,Q板中心有一小孔,P板上与小孔正对的位置有一个粒子源S,从S处可以发出初速度为0、带电量为+q、质量为m的粒子,这些粒子与三棱柱侧面碰撞时无能量损失.试求: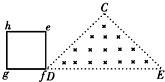 如图甲所示,在虚线所示的等腰直角三角形CDE(其底边DE长为3L)区域内,存在有垂直纸面向里的匀强磁场,一边长为L的正方形线框efgh(gf边与DE边在同一直线上)在纸平面内沿DE方向从左向右以速度v匀速通过场区.若以图示位置为计时起点,规定逆时针方向为线框中感应电流的正方向,则图乙所示的四个i-t图象(横轴单位长度表示的值为L/v),哪一个能反映线框中感应电流的规律( )
如图甲所示,在虚线所示的等腰直角三角形CDE(其底边DE长为3L)区域内,存在有垂直纸面向里的匀强磁场,一边长为L的正方形线框efgh(gf边与DE边在同一直线上)在纸平面内沿DE方向从左向右以速度v匀速通过场区.若以图示位置为计时起点,规定逆时针方向为线框中感应电流的正方向,则图乙所示的四个i-t图象(横轴单位长度表示的值为L/v),哪一个能反映线框中感应电流的规律( )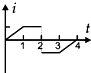
 (2013?普陀区二模)在“利用单摆测重力加速度”的实验中:
(2013?普陀区二模)在“利用单摆测重力加速度”的实验中: