题目内容
10.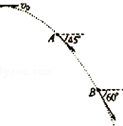 如图所示,某一小球以v0=5m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球速度方向与水平方向的夹角为45°,在B点小球速度方向与水平方向的夹角为60°(空气阻力忽略不计,g取10m/s2).以下判断中正确的是( )
如图所示,某一小球以v0=5m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球速度方向与水平方向的夹角为45°,在B点小球速度方向与水平方向的夹角为60°(空气阻力忽略不计,g取10m/s2).以下判断中正确的是( )| A. | 小球经过A、B两点间的时间t=($\sqrt{3}$-1)s | B. | 小球经过A、B两点间的时间t=$\sqrt{3}$s | ||
| C. | A、B两点间的高度差h=10m | D. | A、B两点间的高度差h=2.5m |
分析 根据平行四边形定则求出A、B的竖直分速度,结合速度时间公式求出小球由A到B的时间.根据速度位移公式求出A、B的高度差.
解答 解:AB、根据平行四边形定则知,A、B两点处竖直分速度大小分别为 vyA=v0=5m/s,vyB=v0tan60°=$\sqrt{3}$v0,
则小球由A到B的时间 t=$\frac{{v}_{yB}-{v}_{yA}}{g}$=$\frac{(\sqrt{3}-1){v}_{0}}{g}$=$\frac{\sqrt{3}-1}{2}$s.故A、B错误.
CD、A、B的高度差 h=$\frac{{v}_{yB}^{2}-{v}_{yA}^{2}}{2g}$=$\frac{{v}_{0}^{2}}{g}$=$\frac{{5}^{2}}{10}$m=2.5m,故C错误,D正确.
故选:D.
点评 解决本题的关键掌握平抛运动的研究方法:运动的分解,知道平抛运动在水平方向和竖直方向上的运动规律,运用运动学公式进行求解.

练习册系列答案
相关题目
1. 运动员手持网球拍托球沿水平面匀加速跑,设球拍和球质量分别为M、m球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )
运动员手持网球拍托球沿水平面匀加速跑,设球拍和球质量分别为M、m球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )
 运动员手持网球拍托球沿水平面匀加速跑,设球拍和球质量分别为M、m球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )
运动员手持网球拍托球沿水平面匀加速跑,设球拍和球质量分别为M、m球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )| A. | 运动员的加速度为gcotθ | |
| B. | 球拍对球的作用力$\frac{mg}{cosθ}$ | |
| C. | 运动员对球拍的作用力为Mgcosθ | |
| D. | 若加速度大于gsinθ,球一定沿球拍向上运动 |
18.2011年12月5日美国航天局宣布,科学家们利用“开普勒”太空望远镜在距地球约600光年的一个恒星系统中新发现了一颗宜居行星,代号为“开普勒-22b”,它也是迄今发现的最小且最适于表面存在液态水的行星.假设其半径约为地球的a倍,质量为地球的b倍,则该行星表面由引力产生的加速度g′与地球表面的重力加速度g的比值为( )
| A. | $\frac{a}{b}$ | B. | $\frac{b}{a}$ | C. | $\frac{a}{{b}^{2}}$ | D. | $\frac{b}{{a}^{2}}$ |
5.在离地面80m处无初速释放一小球,小球质量为m=200g,不计空气阻力,g取10m/s2,取最高点所在水平面为参考平面,则第2s末小球的重力势能为( )
| A. | 40J | B. | -40J | C. | 120J | D. | -120J |
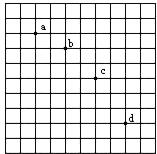 在研究平抛物体运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=0.40cm,若小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为v0=$2\sqrt{gL}$(用L、g表示),其值是0.4m/s.小球在b点的速率vb=0.5m/s.(取g=10m/s2).
在研究平抛物体运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=0.40cm,若小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为v0=$2\sqrt{gL}$(用L、g表示),其值是0.4m/s.小球在b点的速率vb=0.5m/s.(取g=10m/s2).