题目内容
19.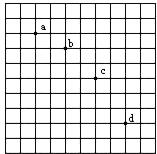 在研究平抛物体运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=0.40cm,若小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为v0=$2\sqrt{gL}$(用L、g表示),其值是0.4m/s.小球在b点的速率vb=0.5m/s.(取g=10m/s2).
在研究平抛物体运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=0.40cm,若小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为v0=$2\sqrt{gL}$(用L、g表示),其值是0.4m/s.小球在b点的速率vb=0.5m/s.(取g=10m/s2).
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据竖直方向上连续相等时间内的位移之差是一恒量求出相等的时间间隔,结合水平位移和时间间隔求出初速度的表达式,从而得出初速度的大小.
解答 解:在竖直方向上,根据△y=L=gT2得,T=$\sqrt{\frac{L}{g}}$=$\sqrt{\frac{0.4×1{0}^{-2}}{10}}=0.02s$,
则初速度${v}_{0}=\frac{2L}{T}=2\sqrt{gL}$,
带入数据得:${v}_{0}=2×\sqrt{0.4×1{0}^{-2}×10}=0.4m/s$.
小球在b点的竖直方向速度${v}_{y}=\frac{{h}_{ac}}{2T}=\frac{3×0.4×1{0}^{-2}}{0.04}=0.3m/s$,
则b点速率vb=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=0.5m/s$
故答案为:$2\sqrt{gL}$;0.4;0.5
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和推论灵活求解,基础题

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
9.小灯泡灯丝的电阻随温度的升高而变大,某同学利用实验探究这一现象.所提供的器材有:
该同学选择仪器,设计电路并进行实验,通过实验得到如下数据:
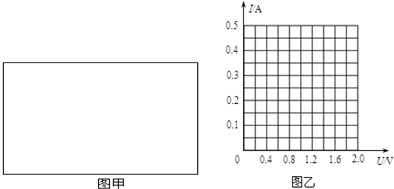
(1)请你推测该同学选择的器材是:电流表为A,电压表为C,滑动变阻器为E(以上均填写器材代号).
(2)请你推测该同学设计的实验电路图并画在图甲的方框中.
(3)请在图乙的坐标系中画出小灯泡的I-U曲线.
(4)若将该小灯泡直接接在电动势是2.0V,内阻是 2.0Ω的电池两端,小灯泡的实际功率为0.50W.
| 代号 | 器材规格 |
| A | 电流表(A1)量程0-0.6A,内阻约0.125Ω |
| B | 电流表(A2)量程0-3A,内阻约0.025Ω |
| C | 电压表(V1),量程0-3V,内阻约3kΩ |
| D | 电压表(V2),量程0-15V,内阻约15kΩ |
| E | 滑动变阻器(R1)总阻值约10Ω |
| F | 滑动变阻器(R2)总阻值约200Ω |
| G | 电池(E)电动势3.0V,内阻很小 |
| H | 导线若干,电键K |
| $\frac{I}{A}$ | 0 | 0.12 | 0.21 | 0.29 | 0.34 | 0.38 | 0.42 | 0.45 | 0.47 | 0.49 | 0.50 |
| $\frac{U}{V}$ | 0 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 |

(1)请你推测该同学选择的器材是:电流表为A,电压表为C,滑动变阻器为E(以上均填写器材代号).
(2)请你推测该同学设计的实验电路图并画在图甲的方框中.
(3)请在图乙的坐标系中画出小灯泡的I-U曲线.
(4)若将该小灯泡直接接在电动势是2.0V,内阻是 2.0Ω的电池两端,小灯泡的实际功率为0.50W.
10.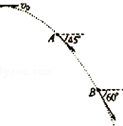 如图所示,某一小球以v0=5m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球速度方向与水平方向的夹角为45°,在B点小球速度方向与水平方向的夹角为60°(空气阻力忽略不计,g取10m/s2).以下判断中正确的是( )
如图所示,某一小球以v0=5m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球速度方向与水平方向的夹角为45°,在B点小球速度方向与水平方向的夹角为60°(空气阻力忽略不计,g取10m/s2).以下判断中正确的是( )
 如图所示,某一小球以v0=5m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球速度方向与水平方向的夹角为45°,在B点小球速度方向与水平方向的夹角为60°(空气阻力忽略不计,g取10m/s2).以下判断中正确的是( )
如图所示,某一小球以v0=5m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球速度方向与水平方向的夹角为45°,在B点小球速度方向与水平方向的夹角为60°(空气阻力忽略不计,g取10m/s2).以下判断中正确的是( )| A. | 小球经过A、B两点间的时间t=($\sqrt{3}$-1)s | B. | 小球经过A、B两点间的时间t=$\sqrt{3}$s | ||
| C. | A、B两点间的高度差h=10m | D. | A、B两点间的高度差h=2.5m |
14. 如图所示,甲、乙两球质量分别为lkg、3kg,它们在光滑水平面上发生正碰,图甲表示甲球碰撞前后的位移-时间图线,图乙表示乙球碰后的位移-时间图线,不计碰撞时间,则下列说法错误的是( )
如图所示,甲、乙两球质量分别为lkg、3kg,它们在光滑水平面上发生正碰,图甲表示甲球碰撞前后的位移-时间图线,图乙表示乙球碰后的位移-时间图线,不计碰撞时间,则下列说法错误的是( )
 如图所示,甲、乙两球质量分别为lkg、3kg,它们在光滑水平面上发生正碰,图甲表示甲球碰撞前后的位移-时间图线,图乙表示乙球碰后的位移-时间图线,不计碰撞时间,则下列说法错误的是( )
如图所示,甲、乙两球质量分别为lkg、3kg,它们在光滑水平面上发生正碰,图甲表示甲球碰撞前后的位移-时间图线,图乙表示乙球碰后的位移-时间图线,不计碰撞时间,则下列说法错误的是( )| A. | 碰撞前乙球的速度可能不等于零 | B. | 碰撞前乙球的速度一定等于零 | ||
| C. | 碰撞后甲球的速度反向了 | D. | 甲、乙两球在t=2s时发生碰撞 |
11.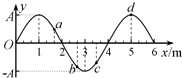 一列简谐横波沿x轴正方向传播,某时刻(t=0)其波形如图所示,a、b、c、d是四个质点,振幅为A.下列说法中正确的是( )
一列简谐横波沿x轴正方向传播,某时刻(t=0)其波形如图所示,a、b、c、d是四个质点,振幅为A.下列说法中正确的是( )
 一列简谐横波沿x轴正方向传播,某时刻(t=0)其波形如图所示,a、b、c、d是四个质点,振幅为A.下列说法中正确的是( )
一列简谐横波沿x轴正方向传播,某时刻(t=0)其波形如图所示,a、b、c、d是四个质点,振幅为A.下列说法中正确的是( )| A. | 该时刻以后,质点a比质点b先到达平衡位置 | |
| B. | 该时刻以后的$\frac{1}{4}$周期内,质点d通过的路程等于A | |
| C. | 该时刻以后的$\frac{1}{4}$周期内,质点a沿波的传播方向移动1m | |
| D. | 该时刻以后的$\frac{1}{4}$周期内,质点b通过的路程比质点c通过的路程大 |
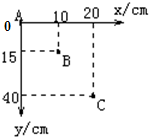 在该实验中,某同学记录了A、B、C三点,取A点为坐标原点,建立了图所示的坐标系.平抛轨迹上的这三点坐标值图中已标出.那么A、B两点的时间间隔是0.1s,小球平抛的初速度为1m/s.(g=10m/s2)
在该实验中,某同学记录了A、B、C三点,取A点为坐标原点,建立了图所示的坐标系.平抛轨迹上的这三点坐标值图中已标出.那么A、B两点的时间间隔是0.1s,小球平抛的初速度为1m/s.(g=10m/s2)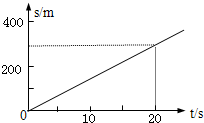
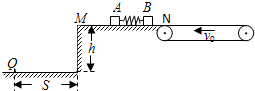 如图所示,光滑水平台面MN上放两个相同小物块A、B,右端N处与水平传送带理想连接,传送带水平部分长度L=10m,沿逆时针方向以恒定速度v0=2m/s匀速转动.物块A、B(大小不计,视作质点)与传送带间的动摩擦因数均为μ=0.2,物块A、B质量分别为mA=3kg、mB=2kg,开始时A、B静止,A、B间压缩一轻质短弹簧.现解除锁定,弹簧弹开A、B,弹开后B滑上传送带,A掉落到地面上的Q点,已知水平台面高h=0.8m,Q点与水平台面间右端间的距离S=1.6m,g取10m/s2.求:
如图所示,光滑水平台面MN上放两个相同小物块A、B,右端N处与水平传送带理想连接,传送带水平部分长度L=10m,沿逆时针方向以恒定速度v0=2m/s匀速转动.物块A、B(大小不计,视作质点)与传送带间的动摩擦因数均为μ=0.2,物块A、B质量分别为mA=3kg、mB=2kg,开始时A、B静止,A、B间压缩一轻质短弹簧.现解除锁定,弹簧弹开A、B,弹开后B滑上传送带,A掉落到地面上的Q点,已知水平台面高h=0.8m,Q点与水平台面间右端间的距离S=1.6m,g取10m/s2.求: