Question

【题目】一光滑斜面固定在水平地面上，用平行于斜面的力F拉质量为m的物体，可使它匀速向上滑动，如图所示、若改用大小为3F的力，仍平行于斜面向上拉该物体，让物体从底部由静止开始运动、已知斜面长为L，物体的大小可以忽略、求：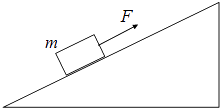

（1）在3F力的作用下，物体到达斜面顶端时的速度；
（2）要使物体能够到达斜面顶端，3F力作用的时间至少多长？

Answer 1

【答案】
（1）解：设斜面倾角为θ，在物体匀速运动时，对物体受力分析可得：

F﹣mgsinθ=0

当用3F的拉力时，设物体的加速度为a，到达顶端时速度为V，

由牛顿第二定律可得：

3F﹣mgsinθ=ma

由速度位移的关系式可得：

v2﹣0=2aL

解得：v=2

答：所以物体到达斜面顶端的速度为2

（2）解：设3F的拉力至少作用t1时间，加速度为a1，撤去后加速度大小为a2

由牛顿第二定律可得：

3F﹣mgsinθ=ma1

F=mgsinθ=ma2

物体加速上升的位移为：

S1= a1t12

物体减速上升的位移为：

S2=Vt﹣ a2t22

物体运动的总位移等于斜面的长度L，

即：S1+S2=L

因为加速的末速度就是减速过程的初速度，

即：V=a1t1=a2t2

由以上方程联立解得：t1=

答：3F力作用的时间为

【解析】（1）由于物体匀速运动，对物体受力分析可以得到F与重力的关系，再由牛顿第二定律求得加速度，根据速度位移的关系式可以求得物体到达斜面顶端的速度；（2）物体的加速运动和减速运动的总位移就是斜面的长度，根据位移公式可以求得物体加速运动的时间．