题目内容
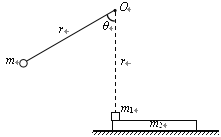
【题目】在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6.0×105 N/C,方向与x轴正方向相同。在O处放一个电荷量q=-5.0×10-8 C,质量m=1.0×10-2 kg的绝缘物块。物块与水平面间的动摩擦因数μ=0.20,沿x轴正方向给物块一个初速率v0=2.0 m/s,如图所示。(g取10 m/s2)试求:
(1)物块向右运动的最大距离;
(2)物块最终停止的位置。

【答案】(1)0.4 m; (2)O点左侧0.2 m处;
【解析】试题分析:(1)设物块向右运动的最大距离为xm,由动能定理得:-μmgxm-E|q|xm=0-![]() ,
,
求得:xm="0.4" m
(2)因Eq>μmg,物块不可能停止在O点右侧,设最终停在O点左侧且离O点为x处,由动能定理得:E|q|xm-μmg(xm+x)=0 ,可得:x=0.2m

练习册系列答案
相关题目
【题目】某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点。其相邻点间的距离如图所示,每两个相邻的测量点之间的时间间隔为0.1s。
(1)试根据纸带上各个计数点间的距离,每个0.10s测一次速度,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并将各个速度值填入下表(要求保留3位有效数字)

______;______;_______;________;_________;
VB | VC | VD | VE | VF | |
时间(t/s) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
速度(m/s) |

(2)将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并画出小车的瞬时速度随时间变化的关系图线___________。