题目内容
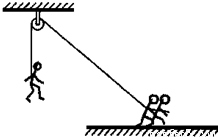
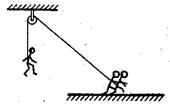
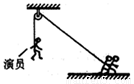
(14分)如图所示,地面上的人通过定滑轮用轻绳将质量为m=40kg的演员从静止开始沿竖直方向向上拉起,演员先做匀加速直线运动,再做匀减速直线运动直到静止。演员加速运动与减速运动过程中的加速度大小之比为1:4,全过程用时t=l0s,上升的高度h=l0m。忽略滑轮的质量及摩擦,求在演员上升过程中,绳子拉力对演员做功的最大功率(重力加速度g取l0m/s2).
【答案】
820W
【解析】
试题分析:设演员在匀加速和匀减速时间分别是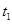 和
和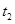 ,加速度大小分别是
,加速度大小分别是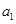 和
和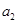 ,最大速度为
,最大速度为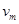 ,如图所示,
,如图所示,
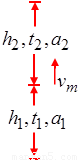
由题设知:
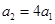

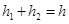
由运动学规律得:
加速阶段 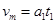
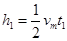
减速阶段 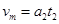
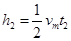
联立以上各式解得 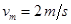
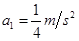
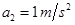
根据题设条件知匀加速运动结束时速度达最大,此时拉力对演员做功的最大功率.设演员加速上升过程中绳子的拉力为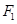 ,拉力对演员做功的最大功率为
,拉力对演员做功的最大功率为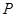 ,则
,则
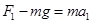
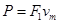
解得: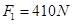
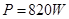
故在演员上升过程中,绳子拉力对演员做功的最大功率为820N
考点:本题考查了牛顿第二定律;功率;匀变速直线运动的速度与时间的关系;匀变速直线运动的位移与时间的关系.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
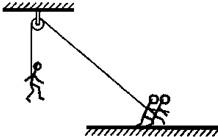 2010年11月广州亚运会开幕式文艺表演最震撼人心的节目当数《白云之帆》篇章,是由地面上近1400人用绳索拉着的180名演员上演着“空中飞人”.九分钟的时间里,180名塔沟武校的武林小子在帆屏上时而俯冲而下,时而攀沿升空,演绎了一场世所罕见的惊险、刺激却又浪漫、温馨的节目.现在把他们某次训练过程中的情节简化成如下模型:如图所示,地面上的人通过定滑轮用轻绳将质量m=60kg的演员从静止竖直向上拉高24m,用时t=6s,演员在竖直方向上先做匀加速直线运动,再做匀减速直线运动后静止在高空.其加速和减速过程中的加速度之比为1:5,忽略滑轮的质量和滑轮与轴之间的摩擦力.求演员在匀加速上升过程中绳子对地面上的人的拉力为多少?(g=10m/s2)
2010年11月广州亚运会开幕式文艺表演最震撼人心的节目当数《白云之帆》篇章,是由地面上近1400人用绳索拉着的180名演员上演着“空中飞人”.九分钟的时间里,180名塔沟武校的武林小子在帆屏上时而俯冲而下,时而攀沿升空,演绎了一场世所罕见的惊险、刺激却又浪漫、温馨的节目.现在把他们某次训练过程中的情节简化成如下模型:如图所示,地面上的人通过定滑轮用轻绳将质量m=60kg的演员从静止竖直向上拉高24m,用时t=6s,演员在竖直方向上先做匀加速直线运动,再做匀减速直线运动后静止在高空.其加速和减速过程中的加速度之比为1:5,忽略滑轮的质量和滑轮与轴之间的摩擦力.求演员在匀加速上升过程中绳子对地面上的人的拉力为多少?(g=10m/s2)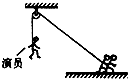 如图所示,地面上的人通过定滑轮用轻绳将质量为m=40kg的演员从静止开始沿竖直方向向上拉起,演员先做匀加速直线运动,再做匀减速直线运动直到静止.演员加速运动与减速运动过程中的加速度大小之比为1:4,全过程用时t=l0s,上升的高度h=l0m.忽略滑轮的质量及摩擦,求在演员上升过程中,绳子拉力对演员做功的最大功率(重力加速度g取l0m/s2).
如图所示,地面上的人通过定滑轮用轻绳将质量为m=40kg的演员从静止开始沿竖直方向向上拉起,演员先做匀加速直线运动,再做匀减速直线运动直到静止.演员加速运动与减速运动过程中的加速度大小之比为1:4,全过程用时t=l0s,上升的高度h=l0m.忽略滑轮的质量及摩擦,求在演员上升过程中,绳子拉力对演员做功的最大功率(重力加速度g取l0m/s2).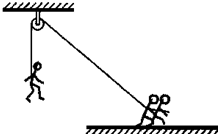 在大型文艺节目《白云之帆》表演中,由地面上近1200人用绳索拉着180名演员上演着“空中飞人”.九分钟的时间里,180名塔沟武校的武林小子在帆屏上时而俯冲而下,时而攀沿升空,演绎了一场世界罕见的惊险、刺激却又浪漫、温馨的节目.现在把他们某次训练过程中的情节简化成如下模型:如图所示,地面上的人通过定滑轮用轻绳将质量m=50kg的演员从静止竖直向上拉高28m,用时t=7s,演员在竖直方向上先做匀加速直线运动,再做匀减速直线运动后静止在高空.其加速和减速过程中的加速度之比为2:5,忽略滑轮的质量和滑轮与轴之间的摩擦力.求:
在大型文艺节目《白云之帆》表演中,由地面上近1200人用绳索拉着180名演员上演着“空中飞人”.九分钟的时间里,180名塔沟武校的武林小子在帆屏上时而俯冲而下,时而攀沿升空,演绎了一场世界罕见的惊险、刺激却又浪漫、温馨的节目.现在把他们某次训练过程中的情节简化成如下模型:如图所示,地面上的人通过定滑轮用轻绳将质量m=50kg的演员从静止竖直向上拉高28m,用时t=7s,演员在竖直方向上先做匀加速直线运动,再做匀减速直线运动后静止在高空.其加速和减速过程中的加速度之比为2:5,忽略滑轮的质量和滑轮与轴之间的摩擦力.求: